
【题目】在等边△ABC中.
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.

【答案】(1)80°(2)①见解析(2)证明见解析
【解析】
(1)根据等边三角形的性质得到∠B=60°,由三角形的外角等于不相邻的两个内角和得出∠APC的度数,再由等边对等角即可得出结论;
(2)①根据题意补全图形;
②证明△APM为等边三角形即可得出结论.
(1)∵△ABC为等边三角形,∴∠B=60°,∴∠APC=∠BAP+∠B=80°.
∵AP=AQ,∴∠AQB=∠APC=80°.
(2)① 补全图形如图所示.
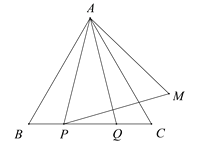
②过点A作AH⊥BC于点H,如图,∵△ABC为等边三角形,AP=AQ,∴∠PAH=∠QAH,∠BAH=∠CAH,∴∠PAB=∠QAC.
∵点Q,M关于直线AC对称,∴∠QAC=∠MAC,AQ=AM,∴∠PAB=∠MAC,AP=AM.
∵∠BAC=60°,∴∠PAM=∠BAC=60°.
∵AP=AM,∴△APM为等边三角形,∴PA=PM.


科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们设[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1-m,-1-m]的函数的若干结论:
①当m=-3时,该函数图象的顶点坐标是(![]() ,
,![]() );
);
②当m=1时,该函数图象截x轴所得的线段的长度为2;
③当m=-1时,该函数在x>![]() 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,该函数图象必经过x轴上的一个定点.
上述结论中正确的有_________________.(只需填写所有正确答案的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形ABC的边长为7,点D为AB上一点,点E在BC的延长线上,且CE=AD,连接DE交AC于点F,作DH⊥AC于点H,则线段HF的长为 ____________.
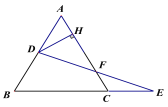
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小李从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为35 m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2m,现己知购买这种铁皮每平方米需30元钱,问小李购回这张矩形铁皮共花了多少元钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB=4,另有一块等腰直角三角板的直角顶点放在C处,CP=CQ=2,将三角板CPQ绕点C旋转(保持点P在△ABC内部),连接AP、BP、BQ.
(1)如图1求证:AP=BQ;
(2)如图2当三角板CPQ绕点C旋转到点A、P、Q在同一直线时,求AP的长;
(3)设射线AP与射线BQ相交于点E,连接EC,写出旋转过程中EP、EQ、EC之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
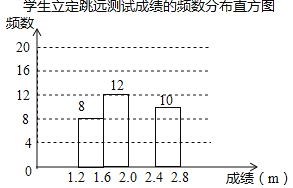
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:把![]() 和
和![]() 按如图甲摆放(点
按如图甲摆放(点![]() 与点
与点![]() 重合),点
重合),点![]() 、
、![]() 、
、![]() 在同一条直线上.
在同一条直线上.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如图乙,
.如图乙,![]() 从图甲的位置出发,以
从图甲的位置出发,以![]() 的速度沿
的速度沿![]() 向
向![]() 匀速移动,在
匀速移动,在![]() 移动的同时,点
移动的同时,点![]() 从
从![]() 的顶点
的顶点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动.当点
匀速移动.当点![]() 移动到点
移动到点![]() 时,
时,![]() 点停止移动,
点停止移动,![]() 也随之停止移动.
也随之停止移动.![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() 、
、![]() ,设移动时间为
,设移动时间为![]() .解答下列问题:
.解答下列问题:
![]() 设三角形
设三角形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 当
当![]() 为何值时,三角形
为何值时,三角形![]() 为等腰三角形?
为等腰三角形?
![]() 是否存在某一时刻
是否存在某一时刻![]() ,使
,使![]() 、
、![]() 、
、![]() 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知CF是△ABC的外角∠ACE的角平分线,D为CF上一点,且DA=DB.

(1)求证:∠ACB=∠ADB;
(2)求证:AC+BC<2BD;
(3)如图2,若∠ECF=60°,证明:AC=BC+CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com