
����Ŀ����֪������y=a��x+3����x��1����a��0������x��������������ཻ��A��B���㣬��y���ཻ�ڵ�C��������A��ֱ��y=�� ![]() x+b�������ߵ���һ������ΪD��
x+b�������ߵ���һ������ΪD��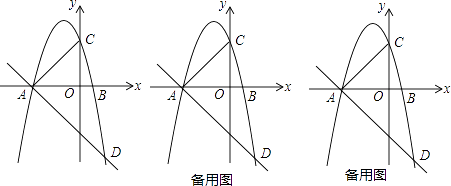
��1������D�ĺ�����Ϊ2���������ߵĺ�������ʽ��
��2�����ڵ��������ڵ����������е�P��ʹ����A��B��PΪ��������������ABC���ƣ����P�����ꣻ
��3���ڣ�1���������£����E���߶�AD�ϵ�һ�㣨�����˵㣩������BE��һ����Q�ӵ�B���������߶�BE��ÿ��1����λ���ٶ��˶�����E�������߶�ED��ÿ�� ![]() ����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
���𰸡�
��1��
�⣺��y=a��x+3����x��1����
���A����������3��0������B����������1��0����
��ֱ��y=�� ![]() x+b������A��
x+b������A��
��b=��3 ![]() ��
��
��y=�� ![]() x��3
x��3 ![]() ��
��
��x=2ʱ��y=��5 ![]() ��
��
���D��������2����5 ![]() ����
����
�ߵ�D���������ϣ�
��a��2+3����2��1��=��5 ![]() ��
��
��ã�a=�� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() ��x+3����x��1��=��
��x+3����x��1��=�� ![]() x2��2
x2��2 ![]() x+3
x+3 ![]()
��2��
�⣺ 
��PH��x����H��
���P��������m��n����
����BPA�ס�ABCʱ����BAC=��PBA��
��tan��BAC=tan��PBA���� ![]() ��
��
�� ![]() ����n=��a��m��1����
����n=��a��m��1����
�� ![]() ��
��
��ã�m1=��4��m2=1���������⣬��ȥ����
��m=��4ʱ��n=5a��
�ߡ�BPA�ס�ABC��
�� ![]() ����AB2=ACPB��
����AB2=ACPB��
��42= ![]()
![]() ��
��
��ã�a1= ![]() ���������⣬��ȥ����a2=��
���������⣬��ȥ����a2=�� ![]() ��
��
��n=5a=�� ![]() ��
��
���P����������4���� ![]() ����
����
����PBA�ס�ABCʱ����CBA=��PBA��
��tan��CBA=tan��PBA���� ![]() ��
��
�� ![]() ����n=��3a��m��1����
����n=��3a��m��1����
�� ![]() ��
��
��ã�m1=��6��m2=1���������⣬��ȥ����
��m=��6ʱ��n=21a��
�ߡ�PBA�ס�ABC��
�� ![]() ����AB2=BCPB��
����AB2=BCPB��
��42= ![]()
![]() ��
��
��ã�a1= ![]() ���������⣬��ȥ����a2=��
���������⣬��ȥ����a2=�� ![]() ��
��
���P����������6���� ![]() ����
����
�������������������ĵ�P������Ϊ����4���� ![]() ���ͣ���6����
���ͣ���6���� ![]() ��
��
��3��
�⣺ 
��DM��x�ύ��������M����DN��x����N����EF��DM��F��
��tan��DAN= ![]() =
= ![]() ��
��
���DAN=60�㣬
���EDF=60�㣬
��DE= ![]() EF��
EF��
��Q���˶�ʱ��t= ![]() =BE+EF��
=BE+EF��
�൱BE��EF����ʱ��t��С��
��BE��DM��y=��4 ![]() ��
��
����������1�����ݶ��κ����Ľ���ʽȷ����A��B�����꣬���ֱ�ߵĽ���ʽ�������D�����꣬��������ߵĽ���ʽ����2����PH��x����H�����P������Ϊ��m��n�����֡�BPA�ס�ABC�͡�PBA�ס�ABC���������������ε����ʼ��㼴�ɣ���3����DM��x�ύ��������M����DN��x����N����EF��DM��F���������еĶ������Q���˶�ʱ��t=BE+EFʱ��t��С���ɣ����⿼����Ƕ��κ���֪ʶ���ۺ����ã����ն��κ��������ʡ����κ����Ľ���ʽ�����������ε��ж����������ʶ����ǽ���Ĺؼ������ʱ��ע����������˼���������ã�
�����㾫����ͨ��������ö��κ�����ͼ��Ͷ��κ��������ʣ����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����Խ����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����E��F��BD�ϣ�BE=DF�� 
��1����֤��AE=CF��
��2����AB=6����COD=60�㣬�����ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
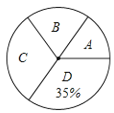
����Ŀ��ij��Ϊ���˽�2018����б�ҵ����ҵ���ȥ�Բ��־��꼶ѧ�������˳������飬�;��꼶ѧ��������ȥ��(A������ͨ���У�B����ְҵ���У�C��ֱ�ӽ�������ҵ��D������)��������ͳ�ƣ���������������������ͳ��ͼ(��ͼ�٢�)���ʣ�

��1�����ι�������_ �����б�ҵ����
��2�����������γ��������У���ְҵ���е���������ռ�ٷֱȣ���������ͳ��ͼ�в������IJ��ֲ���������
��3��������2018����꼶��ҵ������![]() �ˣ�����Ƹ��ؽ�����꼶��ҵ����ְҵ���е�ѧ��������
�ˣ�����Ƹ��ؽ�����꼶��ҵ����ְҵ���е�ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��

��1����ͼ�٣���![]() ��б��
��б��![]() �ϣ��Ե�
�ϣ��Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶��Բ��
��Ϊ�뾶��Բ��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() �����
�����![]() �����ڵ�
�����ڵ�![]() ����֤��
����֤��![]() ��
��
��2����ͼ������![]() ��ʹ����������������
��ʹ����������������
��Բ���ڱ�![]() �ϣ��ھ�����
�ϣ��ھ�����![]() �������
�������![]() ����
����
���߹���ͼ��ֻ������ͼ�ۼ�����Ҫ��д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AC��BC��BD��AD��AC ��BD ����O��AC=BD��
��֤����1��BC=AD��
��2����OAB�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AB=5cm��AC=3cm������P�ӵ�B����������BC��1cm/s���ٶ��ƶ������˶���ʱ��Ϊts��
��1����BC�ߵij���
��2������ABPΪֱ��������ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=�� ![]() x+2
x+2 ![]() ��x�ᣬy��ֱ��ڵ�A����B��������D��E�ֱ�ӵ�A����Bͬʱ�������O�˶����˶�����Oֹͣ�����˶��ٶȷֱ���1����λ����/���
��x�ᣬy��ֱ��ڵ�A����B��������D��E�ֱ�ӵ�A����Bͬʱ�������O�˶����˶�����Oֹͣ�����˶��ٶȷֱ���1����λ����/��� ![]() ����λ����/�룬���˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������Ϊ��G����AB�ཻ�ڵ�F��
����λ����/�룬���˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������Ϊ��G����AB�ཻ�ڵ�F��
��1�����A����B�����ꣻ
��2���ú�t�Ĵ���ʽ�ֱ��ʾEF��AF�ij���
��3�����ı���ADEFΪ����ʱ�����жϡ�AFG���AGB�Ƿ����ƣ���˵�����ɣ�
��4���Ƿ����t��ֵ��ʹ��AGFΪֱ�������Σ������ڣ������ʱ�����ߵĽ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼�ǿ��У���ⰲȫ��أ�����ƽ��У��ijѧУ�ƻ�����15̨��������豸�����мס��������ͺŵ��豸������ÿ̨�۸���Ч��ذ뾶�����ʾ�������飬����1̨�����豸�ȹ���1̨�����豸��150Ԫ������2̨�����豸�ȹ���3̨�����豸��400Ԫ��
���� | ���� | |
�۸�Ԫ/̨�� | a | b |
��Ч�뾶����/̨�� | 150 | 100 |
��1����a��b��ֵ��
��2������������豸���ʽ���11000Ԫ����Ҫ���ذ뾶���Ƿ�Χ������1600�ף������ͺŵ��豸��Ҫ������һ̨������ΪѧУ��ƹ������������������ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��10��21�գ����й������Ƽ�����Ѳչ������ʽ���»�������������ʢ����У��˴�Ѳչ���������ѧ��Ϊ���⣮����ij��ѧ������������֪ʶ��������Ϊ�˽�˴�������֪ʶ�������ɼ�������������ȡ�˲��ֲ���ѧ���ijɼ������������������µIJ�������ͳ�Ʊ���ͳ��ͼ����ͼ��ʾ�������ͼ����Ϣ����������⣮
��� | �ɼ� | Ƶ�� |
A�� |
|
|
B�� |
| 12 |
C�� |
| 18 |
D�� |
| 21 |
��1������һ����ȡ��________������ѧ���ijɼ���![]() ________��
________��
��2�������������ͳ��ͼ����![]() ����Բ�ĽǶ�����
����Բ�ĽǶ�����
��3�����ɼ���90�����ϣ�����90�֣���Ϊ�������ȣ���֪��У����1200��ѧ����������Ƹ�УԼ�ж�����ѧ���ijɼ����������ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com