
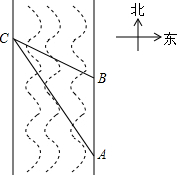
 在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这段河段的宽度.(参考数值:tan31°≈$\frac{3}{5}$)
在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这段河段的宽度.(参考数值:tan31°≈$\frac{3}{5}$) 分析 河宽就是点C到AB的距离,因此过点C作CD⊥AB,垂足为D,根据AB=AD-BD=40米,通过解两个直角三角形分别表示AD、BD的方程求解.
解答 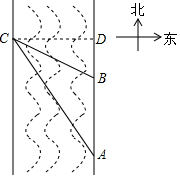 解:过点C作CD⊥AB,垂足为D,
解:过点C作CD⊥AB,垂足为D,
设CD=x米,
在Rt△BCD中,∠CBD=45°,
∴BD=CD=x米.
在Rt△ACD中,∠DAC=31°,
AD=AB+BD=(40+x)米,CD=x米,
∵tan∠DAC=$\frac{CD}{AD}$,
∴$\frac{x}{40+x}$=$\frac{3}{5}$,
解得x=60.
经检验x=60是原方程的解,且符合题意.
点评 本题考查了解直角三角形,“化斜为直”是解三角形的基本思路,因此需作垂线(高)构造直角三角形.


科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
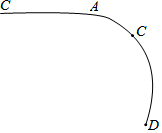 如图,一段圆弧AB上有一个点D,直线AC与圆弧相切于点A,请借助于切点A及B、D两点,利用尺规作图找出这段圆弧所在圆的圆心(不写作法,保留作图痕迹).
如图,一段圆弧AB上有一个点D,直线AC与圆弧相切于点A,请借助于切点A及B、D两点,利用尺规作图找出这段圆弧所在圆的圆心(不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边△ABC的边长为10,D为AC上任意一点,延长AB至点E,使BE=CD,连接DE交BC于点P.
如图,等边△ABC的边长为10,D为AC上任意一点,延长AB至点E,使BE=CD,连接DE交BC于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com