
分析 (1)根据题意4!=4×3×2×1=24;
(2)根据规定2,$\frac{0!}{2!}$=$\frac{1}{2×1}$=$\frac{1}{2}$;
(3)根据规定2,(3+2)!-4!=5!-4!,再运算即可;
(4)用赋值法证明即可;
解答 解:(1)4!=4×3×2×1=24;
(2)$\frac{0!}{2!}$=$\frac{1}{2×1}$=$\frac{1}{2}$;
(3)(3+2)!-4!=5!-4!=5×4×3×2×1-4×3×2×1=120-24=96;
(4)不成立.
如:m=3,n=2时,
3!=3×2×1=6,2!=2,
m!+n!=3!+2!=6+2=8,
(m+n)!=5!=120,
∴(m+n)!=m!+n!不成立.
点评 本题主要考查了数字的变化规律,根据题意发现规律,运用规律是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
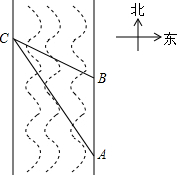 在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这段河段的宽度.(参考数值:tan31°≈$\frac{3}{5}$)
在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这段河段的宽度.(参考数值:tan31°≈$\frac{3}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com