
分析 (1)先把各二次根式化简为最简二次根式,然后合并后进行二次根式的除法运算;
(2)先把各二次根式化简为最简二次根式,然后合并即可;
(3)利用二次根式的乘除法则和二次根式的性质进行运算.
解答 解:(1)原式=$\frac{2\sqrt{2}-3\sqrt{2}}{\sqrt{2}}$
=-1;
(2)原式=10$\sqrt{3}$-4$\sqrt{3}$+3$\sqrt{3}$
=9$\sqrt{3}$;
(3)原式=$\sqrt{\frac{2×6}{3}}$-4
=2-4
=-2.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
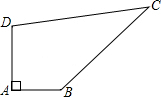 如图,某开发区计划在一块四边形的空地ABCD上种植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,种植每平方米草皮的预算费用为300元,若第一年对草坪的保养费用占种植草皮总预算的4%,以后每年的保养费用都将在前一年的基础上递增2%,求第三年的草坪保养费用.
如图,某开发区计划在一块四边形的空地ABCD上种植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,种植每平方米草皮的预算费用为300元,若第一年对草坪的保养费用占种植草皮总预算的4%,以后每年的保养费用都将在前一年的基础上递增2%,求第三年的草坪保养费用.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
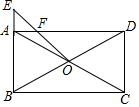 如图,在矩形ABCD中,对角线AC与BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若AB=6,BC=10,AE=2,求AF的长.
如图,在矩形ABCD中,对角线AC与BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若AB=6,BC=10,AE=2,求AF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某小区规划在一个长20米、宽10米的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为27平方米,那么通道的宽应设计成多少米?
如图,某小区规划在一个长20米、宽10米的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为27平方米,那么通道的宽应设计成多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com