
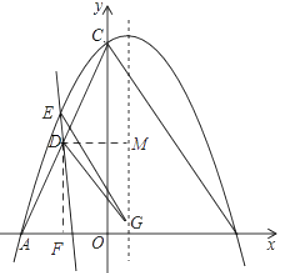
【题目】已知△ABC在平面直角坐标系中的位置如图1所示,A点坐标为(﹣4,0),B点坐标为(6,0),点D为AC的中点,点E是抛物线在第二象限图象上一动点,经过点A,B,C三点的抛物线的解析式为y=ax2+bx+8.
(1)求抛物线的解析式;
(2)如图1,连接DE,把点A沿直线DE翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)图2中,点E运动时,当点G恰好落在BC上时,求E点的坐标.
【答案】
(1)解:∵抛物线y=ax2+bx+8经过点A(﹣4,0),B(6,0),
∴ ![]() ,
,
解得 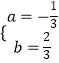 ,
,
∴抛物线的解析式是:y=﹣ ![]() x2+
x2+ ![]() x+8
x+8
(2)解:过点D作DM⊥对称轴于点M,过点D作DF⊥x轴于点F,
令x=0代入y=﹣ ![]() x2+
x2+ ![]() x+8,
x+8,
∴y=8,
∴C(0,8),
∴OC=8,
∵点D为AC的中点,DF∥OC
∴DF是△AOC的中位线,
∴FO=2,DF= ![]() OC=4,
OC=4,
∴D(﹣2,4),
在Rt△AOC中,
由勾股定理可知:AC= ![]() ,
,
∴AD= ![]() AC=2
AC=2 ![]() ,
,
∵点A与点G关于直线DE对称,
∴DG=AD=2 ![]() ,
,
由(1)可知:抛物线y=﹣ ![]() x2+
x2+ ![]() x+8的对称轴为:x=1,
x+8的对称轴为:x=1,
∴M的坐标为(1,4),
∴DM=1﹣(﹣2)=3,
当点G恰好落在抛物线的对称轴上时,
设G点的坐标为(1,n),
∴MG=|4﹣n|,
在Rt△GDM中,DG2=DM2+MG2,
32+(4﹣n)2=20,解得n=4± ![]() ,
,
∴G点的坐标为(1,4+ ![]() )或(1,4﹣
)或(1,4﹣ ![]() )
)
(3)解:当点G恰好落在BC上时,
由对称性可知:AD=DG=CD,
∴A、C、G三点在以D为圆心,AD为半径的圆上,
连接AG, 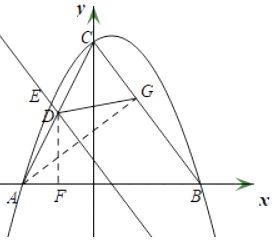
由于AC是⊙D的直径,
∴∠AGC=90°,
∵点A与点G关于ED对称,
∴ED⊥AG,
∴ED∥CG,
设直线BC的解析式为:y=kx+m,
将点C(0.8)、B(6,0)代入y=kx+m,
∴ ![]()
∴解得: 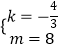 ,
,
∴直线BC的解析式为:y=﹣ ![]() x+8,
x+8,
∴可设直线ED的直线解析式为:y=﹣ ![]() x+d,
x+d,
将D(﹣2,4)代入y=﹣ ![]() x+d,
x+d,
∴4= ![]() +d,
+d,
∴d= ![]() ,
,
∴直线ED的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
联立 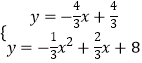
解得:x=3± ![]() ,
,
∵E是抛物线在第二象限图象上一动点,
∴E点的坐标为( ![]() )
)
【解析】(1)把点A和点B的坐标代入抛物线的解析式,得到关于a、b的方程组,从而可求得a与b的值,从而可求出抛物线的解析式;
(2)过点D作DM⊥对称轴于点M,过点D作DF⊥x轴于点F,接下来,求得C、D、M的坐标,从而可求出AD、DM、DG的长度,由于点G在抛物线上,可设G(1,n),最后,再依据勾股定理列方程求解即可;
(3)当点G恰好落在BC上时,由对称性可得到AD=DG=CD,则A、C、G三点在以D为圆心,AD为半径的圆上,连接AG,依据圆周角定理可得到∠AGC=90°,于是可证明ED∥BC,然后再求出直线BC的解析式,从而可求出ED的解析式,最后,联立直线DE的解析式与抛物线的解析式即可求出点E的坐标.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB<BC.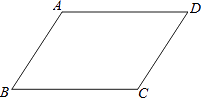
(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC绕着点O按顺时针方向旋转90°后到达△CDE的位置,下列说法中不正确的是( )

A. AB⊥CD
B. AC⊥CE
C. BC⊥DE
D. 点C与点B是两个三角形的对应点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=6,AD=10,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.

(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明;
(4)若点P在C、D两点外侧运动时,请直接写出∠1、∠2、∠3之间的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com