Question

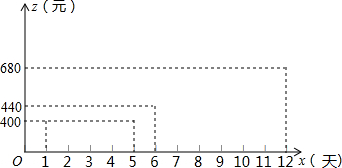
15．在“春季经贸洽谈会”上，我市某服装厂接到生产一批出口服装的订单，要求必须在12天（含12天）内保质保量完成，且当天加工的服装当天立即空运走．为了加快进度，车间采取工人轮流休息，机器满负荷运转的生产方式，生产效率得到了提高．这样每天生产的服装数量y（套）与时间x（元）的关系如表：

时间x（天）	1	2	3	4	…
每天产量y（套）	22	24	26	28	…

由于机器损耗等原因，当每天生产的服装数达到一定量后，平均每套服装的成本会随着服装产量的增加而增大，这样平均每套服装的成本z（元）与生产时间x（天）的关系如图所示．
（1）判断每天生产的服装的数量y（套）与生产时间x（元）之间是我们学过的哪种函数关系？并验证．
（2）已知这批外贸服装的订购价格为每套1570元，设车间每天的利润为w（元）．求w（元）与x（天）之间的函数关系式，并求出哪一天该生产车间获得最高利润，最高利润是多少元？
（3）从第6天起，该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金，但必须保证每天扣除捐款后的利润随时间的增大而增大．求a的最大值，此时留守儿童共得多少元基金？

Answer 1

分析 （1）利用待定系数法求出一次函数解析式，进而验证得出即可；
（2）根据自变量的取值范围，分别求出当1≤x≤5时，以及当6≤x≤12时，求出W的值，即可得出答案；
（3）利用二次函数的性质以及对称轴x=$\frac{970-a}{80}$，在对称轴的左侧，Q随x的增大而增大，求出即可．

解答 解：（1）由表格知，y是x的一次函数，
设y=kx+b，
则$\left\{\begin{array}{l}{k+b=22}\\{2k+b=24}\end{array}\right.$，
∴$\left\{\begin{array}{l}{k=2}\\{b=20}\end{array}\right.$；
∴y=2x+20；
检验：当x=3时，y=2×3+20=26，
当x=4时，y=2×4+20=28，
∴（3，26），（4，28）均满足y=2x+20；

（2）由题意得：z=400（1≤x≤5的整数），
当6≤x≤12的整数时，
设z=k′x+b′，
∴$\left\{\begin{array}{l}{6k′+b′=440}\\{12k′+b′=680}\end{array}\right.$，
∴$\left\{\begin{array}{l}{k′=40}\\{b′=200}\end{array}\right.$．
∴z ₁=40x+200；
当1≤x≤5时．
W ₁=（2x+20）（1570-400），
即W ₁=2340x+23400，
∵2340＞0，
∴W ₁随x的增大而增大．
∴x=5时，
W _1最大=2340×5+23400=35100（元），
当6≤x≤12时，
W ₂=（2x+20）（1570-40x-200）=（2x+20）（1370-40x），
即W ₂=-80x ²+1940x+27400，
∵-80＜0，∴开口向下
对称轴x=-$\frac{1940}{2×（-80）}$=12$\frac{1}{8}$，
在对称轴的左侧，W₂随x的增大而增大．
∴当x=12时，W _2最大=39160（元）
∵39160＞35100，
∴第12天获得最大利润为39160元；

（3）设捐款a元后的利润为Q（元）
∵6≤x≤12，
∴Q=（2x+20）（1570-40x-200-a）
=（2x+20）（1370-2a）x+27400-20a，
∵-80＜0，开口向下，
对称轴x=$\frac{970-a}{80}$，在对称轴的左侧，Q随x的增大而增大．
∴$\frac{970-a}{80}$≥12，
∴a≤10，
∴a的最大值是10，
共得到基金（32+34+36+38+40+42+44）×10=2660（元）．

点评 此题主要考查了一次函数与二次函数的应用，根据已知结合自变量的取值范围确定函数解析式进而求出是解题关键．