
【题目】如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是_____.
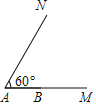
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
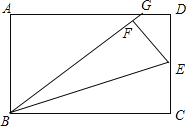
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
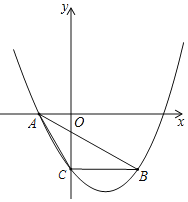
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,与y轴交于点C,连接AB,AC,BC.
两点,与y轴交于点C,连接AB,AC,BC.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 求证:AB平分
求证:AB平分![]() ;
;
![]() 抛物线的对称轴上是否存在点M,使得
抛物线的对称轴上是否存在点M,使得![]() 是以AB为直角边的直角三角形,若存在,求出点M的坐标;若不存在,请说明理由.
是以AB为直角边的直角三角形,若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
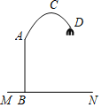
【题目】如图,一款落地灯的灯柱AB垂直于水平地面MN,高度为1.6米,支架部分的形为开口向下的抛物线,其顶点C距灯柱AB的水平距离为0.8米,距地面的高度为2.4 米,灯罩顶端D距灯柱AB的水平距离为1.4米,则灯罩顶端D距地面的高度为______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图:
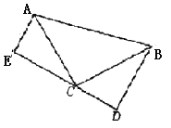
(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;
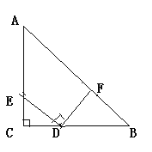
(2)迁移:如图:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F处,则CE=________。(不要求写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
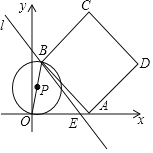
【题目】如图,已知直线l:y=﹣![]() x+8交x轴于点E,点A为x轴上的一个动点(点A不与点E重合),在直线l上取一点B(点B在x轴上方),使BE=5AE,连结AB,以AB为边在AB的右侧作正方形ABCD,连结OB,以OB为直径作⊙P.
x+8交x轴于点E,点A为x轴上的一个动点(点A不与点E重合),在直线l上取一点B(点B在x轴上方),使BE=5AE,连结AB,以AB为边在AB的右侧作正方形ABCD,连结OB,以OB为直径作⊙P.
(1)当点A在点E左侧时,若点B落在y轴上,则AE的长为 ,点D的坐标为 ;
(2)若⊙P与正方形ABCD的边相切于点B,求点B的坐标;
(3)⊙P与直线BE的交点为Q,连结CQ,当CQ平分∠BCD时,BE的长为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
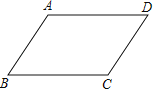
【题目】如图,在平行四边形ABCD中,AD>AB.
(1)作∠BAD的平分线交BC于点E,在AD边上截取AF=AB,连接EF(要求:尺规作图,保留作图痕迹,不写作法);
(2)判断四边形ABEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中考考试中,第一堂语文考试9:00开考,小恺8:00从家出发匀速步行去中考考场,5分钟后,弟弟小熙发现哥哥忘记带准考证,马上沿同一路线匀速送去给哥哥,哥哥到考场门口时发现忘带准考证,马上以之前的速度回家取,途中遇到赶来的弟弟,哥哥拿到准考证后以同样的速度赶往考场,弟弟则回到家中,哥哥与弟弟之间的距离y(米)与弟弟从家出发后步行的时间x(分)之间的关系如图所示(交接准考证的时间忽略不记).则下列结论中,不正确的是( )
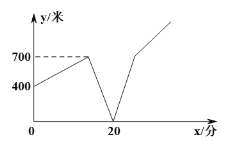
A.弟弟出发20分钟时,将准考证拿给哥哥
B.哥哥出发20分钟到达考场忘记拿准考证
C.哥哥返回考场时,离开考还有30分钟
D.哥哥返回考场时,弟弟离家还有300米
查看答案和解析>>
科目:初中数学 来源: 题型:
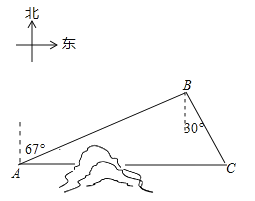
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com