
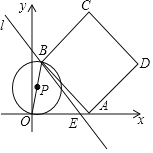
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпlЃКyЃНЉ![]() x+8НЛxжсгкЕуEЃЌЕуAЮЊxжсЩЯЕФвЛИіЖЏЕуЃЈЕуAВЛгыЕуEжиКЯЃЉЃЌдкжБЯпlЩЯШЁвЛЕуBЃЈЕуBдкxжсЩЯЗНЃЉЃЌЪЙBEЃН5AEЃЌСЌНсABЃЌвдABЮЊБпдкABЕФгвВрзїе§ЗНаЮABCDЃЌСЌНсOBЃЌвдOBЮЊжБОЖзїЁбPЃЎ
x+8НЛxжсгкЕуEЃЌЕуAЮЊxжсЩЯЕФвЛИіЖЏЕуЃЈЕуAВЛгыЕуEжиКЯЃЉЃЌдкжБЯпlЩЯШЁвЛЕуBЃЈЕуBдкxжсЩЯЗНЃЉЃЌЪЙBEЃН5AEЃЌСЌНсABЃЌвдABЮЊБпдкABЕФгвВрзїе§ЗНаЮABCDЃЌСЌНсOBЃЌвдOBЮЊжБОЖзїЁбPЃЎ
ЃЈ1ЃЉЕБЕуAдкЕуEзѓВрЪБЃЌШєЕуBТфдкyжсЩЯЃЌдђAEЕФГЄЮЊЁЁ ЁЁЃЌЕуDЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєЁбPгые§ЗНаЮABCDЕФБпЯрЧагкЕуBЃЌЧѓЕуBЕФзјБъЃЛ
ЃЈ3ЃЉЁбPгыжБЯпBEЕФНЛЕуЮЊQЃЌСЌНсCQЃЌЕБCQЦНЗжЁЯBCDЪБЃЌBEЕФГЄЮЊЁЁ ЁЁЃЎЃЈжБНгаДГіД№АИЃЉ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЌЃЈ12ЃЌ4ЃЉЃЛЃЈ2ЃЉТњзуЬѕМўЕФЕуBЕФзјБъЮЊЃЈЉ12ЃЌ24ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉ
ЃЉЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌзїDGЁЭxжсгкGЃЎЭЈЙ§жЄУїЁїOBAЁеЁїDAGМДПЩЕУГіЕуDЕФзјБъЃЛ
ЃЈ2ЃЉЗжШ§жжжжЧщаЮЃКШчЭМ2жаЃЌЕБЕуAгыдЕуOжиКЯЪБЃЌЁбPгыBCЯрЧагкЕуBЃЌAEЃН6ЃЌШчЭМ4жаЃЌЕБOBЁЭABЪБЃЌЁбPгыABЯрЧагкЕуBЃЌзїBHЁЭOAгкHЃЎЗжБ№ЧѓНтМДПЩЃЌШчЭМ4жаЃЌЕБЕуEдкЕуAЕФгвВрЪБЃЌзїBHЁЭOAгкHЃЎРћгУЯрЫЦШ§НЧаЮЕФаджЪЧѓНтМДПЩЃЛ
ЃЈ3ЃЉШчЭМ5ЃЌзїBGЁЭOAгкЕуGЃЌСЌНсOQЃЎЩшAEЃНmЃЌдђBEЃН5mЃЌЕУЕНBGЃН4mЃЌEGЃН3mЃЌAGЃН2mЃЌЧѓЕУBЃЈ6Љ3mЃЌ4mЃЉЃЌCЃЈm+6ЃЌ6mЃЉЃЌAЃЈ6ЉmЃЌ0ЃЉЃЌЕУЕНжБЯпOQЕФНтЮіЪНЮЊ![]() ЃЌЧѓЕУ
ЃЌЧѓЕУ![]() ЃЌЭЦГіCЃЌQЃЌAШ§ЕуЙВЯпЃЌНтЗНГЬМДПЩЕУЕННсТлЃЎ
ЃЌЭЦГіCЃЌQЃЌAШ§ЕуЙВЯпЃЌНтЗНГЬМДПЩЕУЕННсТлЃЎ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌзїDGЁЭxжсгкGЃЎ
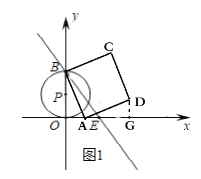
гЩЬтвтЃКEЃЈ6ЃЌ0ЃЉЃЌBЃЈ0ЃЌ8ЃЉЃЌ
ЁрOEЃН6ЃЌOBЃН8ЃЌ
ЁрBEЃН![]() ЃН10ЃЌ
ЃН10ЃЌ
ЁпBEЃН5AEЃЌ
ЁрAEЃН2ЃЌ
ЁрOAЃН4ЃЌ
ЁпЁЯOBA+ЁЯOAB=ЁЯOAB+ЁЯDAG=90,
ЁрЁЯBAOЃНЁЯDAGЃЌ
ЁпAB=DAЃЌЁЯAOBЃНЁЯDGA,
ЁрЁїOBAЁеЁїDAG(AAS)ЃЌ
ЁрDG=OA=4,OB=AG=8ЃЌ
ЁрOG=OA+AG=12,
ЁрDЃЈ12ЃЌ4ЃЉЃЌ
ЙЪД№АИЮЊ2ЃЌЃЈ12ЃЌ4ЃЉЃЛ
ЃЈ2ЃЉШчЭМ2жаЃЌЕБЕуAгыдЕуOжиКЯЪБЃЌЁбPгыBCЯрЧагкЕуBЃЌAEЃН6ЃЌ
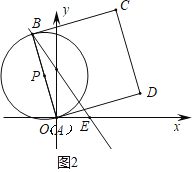
ЁпBEЃН5AEЃЌ
ЁрBEЃН30ЃЌПЩЕУBЃЈЉ12ЃЌ24ЃЉЃЎ
ШчЭМ3жаЃЌЕБOBЁЭABЪБЃЌЁбPгыABЯрЧагкЕуBЃЌзїBHЁЭOAгкHЃЎ
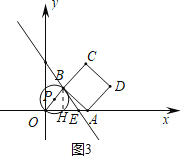
ЩшAEЃНmЃЌдђBEЃН5mЃЌBHЃН4mЃЌEHЃН3mЃЌ
ЁрBHЃНAHЃН4mЃЌ
ЁрЁЯBAOЃН45ЁуЃЌ
ЁпЁЯOBAЃН90ЁуЃЌ
ЁрЁЯBOAЃН45ЁуЃЌ
ЁрЕуBЕФКсзјБъгызнзјБъЯрЭЌЃЌПЩЕУBЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ШчЭМ4жаЃЌЕБЕуEдкЕуAЕФгвВрЪБЃЌзїBHЁЭOAгкHЃЎ
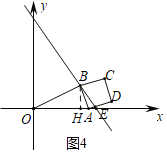
ЩшBEЃН5mЃЌAEЃНmЃЌдђBHЃН4mЃЌAEHЃН3mЃЌAHЃН2mЃЌ
ЁпЁЯOBAЃНЁЯOHBЃН90ЁуЃЌ
гЩЁїOHBЁзЁїBHAЃЌПЩЕУBH2ЃНOHAHЃЌ
Ёр16m2ЃНЃЈ6Љ3mЃЉ2mЃЌ
НтЕУmЃН![]() ЃЌ
ЃЌ
ЁрBЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуBЕФзјБъЮЊЃЈЉ12ЃЌ24ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉШчЭМ5ЃЌзїBGЁЭOAгкЕуGЃЌСЌНсOQЃЎ
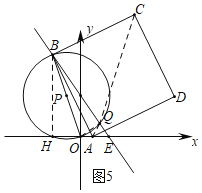
ЩшAEЃНmЃЌдђBEЃН5mЃЌ
ЁрBGЃН4mЃЌEGЃН3mЃЌAGЃН2mЃЌ
ЁрBЃЈ6Љ3mЃЌ4mЃЉЃЌCЃЈm+6ЃЌ6mЃЉЃЌAЃЈ6ЉmЃЌ0ЃЉЃЌ
ЁпOQЁЭжБЯпlЃЌЧвЙ§дВаФOЃЌ
ЁржБЯпOQЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпCQЦНЗжЁЯBCDЃЌ
ЁрCЃЌQЃЌAШ§ЕуЙВЯпЃЌ
Ёр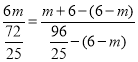 ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
span>Ёр![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ


 УћЪІАщФуГЩГЄПЮЪБЭЌВНбЇСЗВтЯЕСаД№АИ
УћЪІАщФуГЩГЄПЮЪБЭЌВНбЇСЗВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
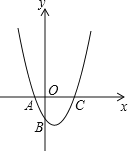
ЁОЬтФПЁПШчЭМЪОЖўДЮКЏЪ§y=ax2+bx+cЕФЖдГЦжсдкyжсЕФгвВрЃЌЦфЭМЯѓгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉгыЕуCЃЈx2ЃЌ0ЃЉЃЌЧвгыyжсНЛгкЕуBЃЈ0ЃЌЉ2ЃЉЃЌаЁЧПЕУЕНвдЯТНсТлЃКЂй0ЃМaЃМ2ЃЛЂкЉ1ЃМbЃМ0ЃЛЂлc=Љ1ЃЛЂмЕБ|a|=|b|ЪБx2ЃО![]() Љ1ЃЛвдЩЯНсТлжае§ШЗНсТлЕФађКХЮЊ ЃЎ
Љ1ЃЛвдЩЯНсТлжае§ШЗНсТлЕФађКХЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
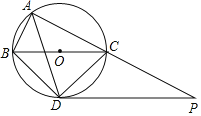
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌЕуOдкBCБпЩЯЃЌЁЯBACЕФЦНЗжЯпНЛЁбOгкЕуDЃЌСЌНгBDЁЂCDЃЌЙ§ЕуDзїBCЕФЦНааЯпгыACЕФбгГЄЯпЯрНЛгкЕуPЃЎ
ЃЈ1ЃЉЧѓжЄЃКPDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїABDЁзЁїDCPЃЛ
ЃЈ3ЃЉЕБAB=5cmЃЌAC=12cmЪБЃЌЧѓЯпЖЮPCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНЃx2ЃЋbxЃЋcОЙ§ЕуB(Ѓ1ЃЌ0)КЭЕуC(2ЃЌ3)ЃЎ
(1)ЧѓДЫХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
(2)ШчЙћДЫХзЮяЯпЩЯЯТЦНвЦКѓЙ§Еу(Ѓ2ЃЌЃ1)ЃЌЧыжБНгаДГіЦНвЦЕФЗНЯђКЭЦНвЦЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯMANЃН60ЁуЃЌШєЁїABCЕФЖЅЕуBдкЩфЯпAMЩЯЃЌЧвABЃН2ЃЌЕуCдкЩфЯпANЩЯдЫЖЏЃЌЕБЁїABCЪЧШёНЧШ§НЧаЮЪБЃЌBCЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
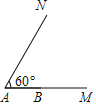
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁИпЗЂЯжЕчЯпИЫ AB ЕФгАзгТфдкЭСЦТЕФЦТУцCDКЭЕиУц BCЩЯЃЌСПЕУ CD= 12 Уз ЃЌ BC= 20 Уз ,CDгыЕиУцГЩ30ЁуНЧЃЌЧвДЫЪБВтЕУ1УзИЫЕФгАГЄЮЊ2 Уз,ЧѓЕчЯпИЫЕФИпЖШЃЎЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтбЇЩњЖдХХЧђЁЂг№УЋЧђЁЂзуЧђЁЂРКЧђЃЈвдЯТЗжБ№гУAЁЂBЁЂCЁЂDБэЪОЃЉетЫФжжЧђРрдЫЖЏЕФЯВКУЧщПіЃЎЖдШЋЬхбЇЩњНјааСЫГщбљЕїВщЃЈУПЮЛбЇЩњжЛФмбЁвЛЯюзюЯВЛЖЕФдЫЖЏЃЉЃЌВЂНЋЕїВщЧщПіЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
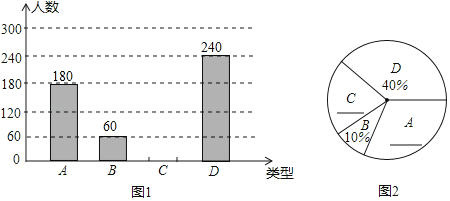
ЧыИљОнвдЩЯаХЯЂЛиД№ЯТУцЮЪЬтЃК
ЃЈ1ЃЉБОДЮВЮМгГщбљЕїВщЕФбЇЩњгаЁЁ ЁЁШЫЃЎ
ЃЈ2ЃЉВЙШЋСНЗљЭГМЦЭМЃЎ
ЃЈ3ЃЉШєДгБОДЮВЮМгГщбљЕїВщЕФбЇЩњжаШЮШЁ1ШЫЃЌдђДЫШЫЯВЛЖФФРрЧђЕФИХТЪзюДѓЃПЧѓЦфИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЧјНЬПЦдКЯыСЫНтИУЧјжаПМЪ§бЇЪдЬтжаЭГМЦЬтЕФЕУЗжЧщПіЃЌДгМзЁЂввСНЫљбЇаЃИїЫцЛњГщШЁСЫ20УћбЇЩњЕФбЇЩњГЩМЈШчЯТЃЎЃЈИУЬтТњЗж10ЗжЃЌбЇЩњЕУЗжОљЮЊећЪ§ЃЉМзбЇаЃ20УћбЇЩњГЩМЈЃЈЕЅЮЛЃКЗжЃЉЗжБ№ЮЊЃК7ЃЌ7ЃЌ8ЃЌ9ЃЌ8ЃЌ6ЃЌ7ЃЌ8ЃЌ8ЃЌ10ЃЌ7ЃЌ9ЃЌ6ЃЌ8ЃЌ7ЃЌ8ЃЌ9ЃЌ7ЃЌ8ЃЌ9ЃЎввбЇаЃ20УћбЇЩњбЇЩњГЩМЈЕФЬѕаЮЭГМЦЭМШчЭМЫљЪОЃК
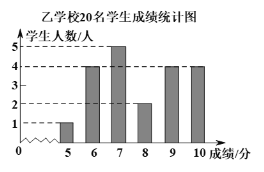
ОЙ§ЖдСНаЃет20УћбЇЩњГЩМЈЕФећРэЃЌЕУЕНЗжЮіЪ§ОнШчЯТБэЃК
зщБ№ | МЋВю | ЦНОљЗж | жаЮЛЪ§ | ЗНВю |
Мз | 4 | b | 8 | 1ЃЎ05 |
вв | a | 7ЃЎ8 | c | 2ЃЎ46 |
ЃЈ1ЃЉЧѓГіБэжаЕФaЁЂbЁЂcЕФжЕЃЎ
ЃЈ2ЃЉИУЬтЕУЗж8ЗжМАЦфвдЩЯМДЮЊгХауЃЌвбжЊМзбЇаЃга1200ШЫЃЌЧыЙРЫуМзбЇаЃЕФгХауШЫЪ§гаЖрЩйШЫЃП
ЃЈ3ЃЉЧыФуНсКЯвдЩЯЗжЮіЪ§ОнЫЕУїЪдЬтжаЭГМЦЬтЕУЗжгХауЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧыДгвдЯТЃЈAЃЉЁЂЃЈBЃЉСНЬтжаШЮбЁвЛИіНтД№ЃЎ
ЃЈAЃЉвбжЊЃКХзЮяЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() КЭЕу
КЭЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊ_____________ЃЛ
ЃЈ2ЃЉЕу![]() ЮЊЕквЛЯѓЯоХзЮяЯпЩЯвЛЕуЃЌЪЧЗёДцдкЪЙ
ЮЊЕквЛЯѓЯоХзЮяЯпЩЯвЛЕуЃЌЪЧЗёДцдкЪЙ![]() УцЛ§зюДѓЕФЕу
УцЛ§зюДѓЕФЕу![]() ЃПШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЌШєДцдкЃЌЧѓГіЕу
ЃПШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЌШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() НЋЯпЖЮ
НЋЯпЖЮ![]() ШЦЦНУцФкФГвЛЕуа§зЊ
ШЦЦНУцФкФГвЛЕуа§зЊ![]() ЕУЯпЖЮ
ЕУЯпЖЮ![]() ЃЈЕу
ЃЈЕу![]() ЗжБ№гыЕу
ЗжБ№гыЕу![]() ЖдгІЃЉЃЌЪЙЕу
ЖдгІЃЉЃЌЪЙЕу![]() ЖМдкХзЮяЯпЩЯЃЌЧыжБНгаДЕу
ЖМдкХзЮяЯпЩЯЃЌЧыжБНгаДЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ЃЈBЃЉШчЭМЃЌвбжЊХзЮяЯп![]() гы
гы![]() жсДгзѓжСгвНЛгк
жсДгзѓжСгвНЛгк![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊ___________:
ЃЈ2ЃЉ![]() ЪЧЕквЛЯѓЯоФкХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЈгыЕу
ЪЧЕквЛЯѓЯоФкХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЈгыЕу![]() ВЛжиКЯЃЉЃЌЙ§Еу
ВЛжиКЯЃЉЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌжБЯп
ЃЌжБЯп![]() ФмЗёАб
ФмЗёАб![]() ЗжГЩУцЛ§жЎБШЮЊ
ЗжГЩУцЛ§жЎБШЮЊ![]() ЕФСНВПЗжЃПШєФмЃЌЧыЧѓГіЕу
ЕФСНВПЗжЃПШєФмЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШє![]() ЮЊХзЮяЯпЖдГЦжсЩЯвЛЖЏЕуЃЌ
ЮЊХзЮяЯпЖдГЦжсЩЯвЛЖЏЕуЃЌ![]() ЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕу
ЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
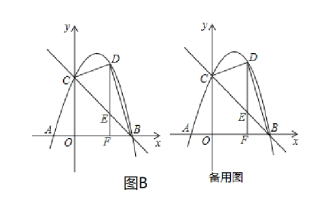
ЮвбЁзіЕФЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com