
【题目】请从以下(A)、(B)两题中任选一个解答.
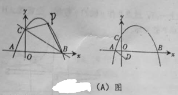
(A)已知:抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)抛物线的解析式为_____________;
(2)点![]() 为第一象限抛物线上一点,是否存在使
为第一象限抛物线上一点,是否存在使![]() 面积最大的点
面积最大的点![]() ?若不存在,请说明理由,若存在,求出点
?若不存在,请说明理由,若存在,求出点![]() 的坐标;
的坐标;
(3)点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() 将线段
将线段![]() 绕平面内某一点旋转
绕平面内某一点旋转![]() 得线段
得线段![]() (点
(点![]() 分别与点
分别与点![]() 对应),使点
对应),使点![]() 都在抛物线上,请直接写点
都在抛物线上,请直接写点![]() 的坐标.
的坐标.
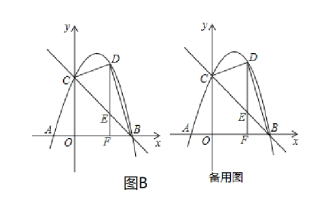
(B)如图,已知抛物线![]() 与
与![]() 轴从左至右交于
轴从左至右交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)抛物线的解析式为___________:
(2)![]() 是第一象限内抛物线上的一个动点(与点
是第一象限内抛物线上的一个动点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() ,直线
,直线![]() 能否把
能否把![]() 分成面积之比为
分成面积之比为![]() 的两部分?若能,请求出点
的两部分?若能,请求出点![]() 的坐标;若不能,请说明理由;
的坐标;若不能,请说明理由;
(3)若![]() 为抛物线对称轴上一动点,
为抛物线对称轴上一动点,![]() 为直角三角形,请直接写出点
为直角三角形,请直接写出点![]() 的坐标.
的坐标.
我选做的是______.
【答案】选B(1)y=-x2+4x+5;(2)能. D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)(2,7),(2,-3),(2,6),(2,-1).
);(3)(2,7),(2,-3),(2,6),(2,-1).
【解析】
选B:(1)把C点坐标代入y=a(x+1)(x-5)中求出a的值即可得到抛物线解析式;
(2)先解方程-(x+1)(x-5)=0得A(-1,0),B(5,0),再利用待定系数法确定直线BC的解析式为y=-x+5,设D(x,-x2+4x+5),则E(x,-x+5),F(x,0),(0<x<5),则DE=-x2+5x,EF=-x+5,利用三角形的面积公式进行讨论:当DE:EF=2:3时,S△BDE:S△BEF=2:3;当DE:EF=3:2时,S△BDE:S△BEF=3:2,从而可得到关于x的方程,然后解方程求出x就看得到对应的D点坐标;
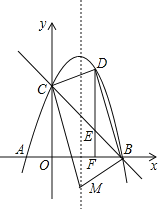
(3)先确定抛物线的对称轴,如图,设M(2,t),利用两点间的距离公式得到BC2=50,MC2=t2-10t+29,MB2=t2+9,利用勾股定理的逆定理分类讨论:当BC2+MC2=MB2时,△BCM为直角三角形,则50+t2-10t+29=t2+9;当BC2+MB2=MC2时,△BCM为直角三角形,则50+t2+9=t2-10t+29;当MC2+MM2=BC2时,△BCM为直角三角形,则t2-10t+29+t2+9=50,然后分别解关于t的方程,从而可得到满足条件的M点坐标.
选B:
(1)把C(0,5)代入y=a(x+1)(x-5)得-5a=5,解得a=-1,
所以抛物线解析式为y=-(x+1)(x-5),即y=-x2+4x+5;
(2)能.
当y=0时,-(x+1)(x-5)=0,解得x1=-1,x2=5,则A(-1,0),B(5,0),
设直线BC的解析式为y=kx+b,
把C(0,5),B(5,0)代入得![]() ,解得
,解得![]() ,
,
所以直线BC的解析式为y=-x+5,
设D(x,-x2+4x+5),则E(x,-x+5),F(x,0),(0<x<5),
∴DE=-x2+4x+5-(-x+5)=-x2+5x,EF=-x+5,
当DE:EF=2:3时,S△BDE:S△BEF=2:3,即(-x2+5x):(-x+5)=2:3,
整理得3x2-17x+10=0,解得x1=![]() ,x2=5(舍去),此时D点坐标为(
,x2=5(舍去),此时D点坐标为(![]() ,
,![]() );
);
当DE:EF=3:2时,S△BDE:S△BEF=3:2,即(-x2+5x):(-x+5)=3:2,
整理得2x2-13x+15=0,解得x1=![]() ,x2=5(舍去),此时D点坐标为(
,x2=5(舍去),此时D点坐标为(![]() ,
,![]() );
);
综上所述,当点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,直线BC能否把△BDF分成面积之比为2:3的两部分;
)时,直线BC能否把△BDF分成面积之比为2:3的两部分;
(3)抛物线的对称轴为直线x=2,如图,
设M(2,t),
∵B(5,0),C(0,5),
∴BC2=52+52=50,MC2=22+(t-5)2=t2-10t+29,MB2=(2-5)2+t2=t2+9,
当BC2+MC2=MB2时,△BCM为直角三角形,∠BCM=90°,即50+t2-10t+29=t2+9,解得t=7,此时M点的坐标为(2,7);
当BC2+MB2=MC2时,△BCM为直角三角形,∠CBM=90°,即50+t2+9=t2-10t+29,解得t=-3,此时M点的坐标为(2,-3);
当MC2+MM2=BC2时,△BCM为直角三角形,∠CMB=90°,即t2-10t+29+t2+9=50,解得t1=6,t2=-1,此时M点的坐标为(2,6)或(2,-1),
综上所述,满足条件的M点的坐标为(2,7),(2,-3),(2,6),(2,-1).


科目:初中数学 来源: 题型:
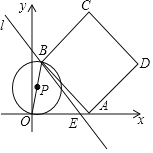
【题目】如图,已知直线l:y=﹣![]() x+8交x轴于点E,点A为x轴上的一个动点(点A不与点E重合),在直线l上取一点B(点B在x轴上方),使BE=5AE,连结AB,以AB为边在AB的右侧作正方形ABCD,连结OB,以OB为直径作⊙P.
x+8交x轴于点E,点A为x轴上的一个动点(点A不与点E重合),在直线l上取一点B(点B在x轴上方),使BE=5AE,连结AB,以AB为边在AB的右侧作正方形ABCD,连结OB,以OB为直径作⊙P.
(1)当点A在点E左侧时,若点B落在y轴上,则AE的长为 ,点D的坐标为 ;
(2)若⊙P与正方形ABCD的边相切于点B,求点B的坐标;
(3)⊙P与直线BE的交点为Q,连结CQ,当CQ平分∠BCD时,BE的长为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料45吨,如果运出甲仓库所存原料的60%,仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库新余的原料多3吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将30吨原料运往工厂,从甲、乙两仓库到工厂的运价分别为120元吨和100元吨.经协商,从甲仓库到工厂的运价可优惠![]() 元吨
元吨![]() ,从乙仓库到工厂的运价不变,设从甲仓库运
,从乙仓库到工厂的运价不变,设从甲仓库运![]() 吨原料到工厂,请求出总运费
吨原料到工厂,请求出总运费![]() 关于
关于![]() 的函数解析式(不要求写出
的函数解析式(不要求写出![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着![]() 的增大,
的增大,![]() 的变化情况.
的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
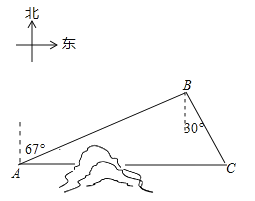
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”小长假期间,小李一家想到以下四个5A级风景区旅游:A.石林风景区;B.香格里拉普达措国家公园;C.腾冲火山地质公园;D.玉龙雪山景区.但因为时间短,小李一家只能选择其中两个景区游玩
(1)若小李从四个景区中随机抽出两个景区,请用树状图或列表法求出所有可能的结果;
(2)在随机抽出的两个景区中,求抽到玉龙雪山风景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
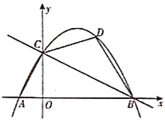
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若点![]() 是抛物线上的一点,且位于直线
是抛物线上的一点,且位于直线![]() 上方,连接
上方,连接![]() ,
,![]() ,
,![]() .当四边形
.当四边形![]() 的面积有最大值时,求点
的面积有最大值时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
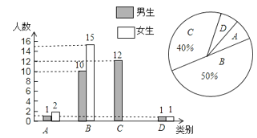
【题目】我县实施新课程改革后,学生的自主字习、合作交流能力有很大提高.某学校为了了解学生自主学习、合作交流的具体情况,对部分学生进行了为期半个月的跟踪调査,并将调査结果分类,A:特别好;B:好;C:一般;D:较差.现将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,一共调査了 名同学,其中C类女生有 名;
(2)将下面的条形统计图补充完整;
(3)为共同进步,学校想从被调査的A类和D类学生中分别选取一位同学进行一帮一互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男生、一位女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题.
定义:如果四边形的某条对角线平分一组对角,那么把这条对角线叫做“美妙线”,该四边形叫做“美妙四边形”.
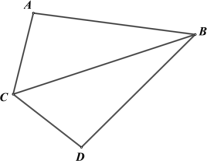
如图,在四边形ABDC中,对角线BC平分∠ACD和∠ABD,那么对角线BC叫“美妙线”,四边形ABDC就称为“美妙四边形”.
问题:
(1)下列四边形:平行四边形、矩形、菱形、正方形,其中是“美妙四边形”的有 个;
(2)四边形ABCD是“美妙四边形”,AB=![]() ∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.(画出图形并写出解答过程)
∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.(画出图形并写出解答过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com