
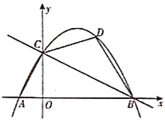
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若点![]() 是抛物线上的一点,且位于直线
是抛物线上的一点,且位于直线![]() 上方,连接
上方,连接![]() ,
,![]() ,
,![]() .当四边形
.当四边形![]() 的面积有最大值时,求点
的面积有最大值时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)把点A、B坐标代入抛物线解析式即可求出a、b的值;
(2)过点D作DF⊥x轴,交BC于点E,先求出直线BC的解析式,设出点D的坐标,再根据D、E横坐标相同求出点E的纵坐标,然后根据“铅锤法”可表示出△BCD的面积,根据二次函数的性质可求出最值,因为△ABC的面积为固定的,故当△BCD面积最大时,则四边形ABCD的面积最大,据此即可求解.
(1)把点A(﹣1,0)、B(4,0)代入抛物线![]() 可得
可得
![]() ,
,
解得:![]() ,
,![]() ,
,
故![]() ,
,![]() .
.
(2)如图,过点D作DF⊥x轴,交BC于点E,
由(1)可知抛物线解析式为: ![]()
令x=0,则y=2
∴点C的坐标(0,2)
设直线![]() 的表达式为
的表达式为![]() ,
,
将![]() ,
,![]() 分别代入,
分别代入,
得![]()
解得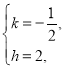
故直线![]() 的表达式为
的表达式为![]() .
.
且当![]() 的面积最大时,四边形
的面积最大时,四边形![]() 的面积最大.
的面积最大.
设![]() ,
,
则E点的横坐标为n,代入直线BC的表达式可得:![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() +
+![]() ,
,
∵S四边形ABCD=S△ABC+S△BCD,且S△ABC为固定值,
∴当S△BCD取得最大值时,S四边形ABCD取得最大值,
∵S△BCD=![]()
根据二次函数的性质可知,当![]() 时,
时,![]() 取最大值,此时S四边形ABCD取得最大值,
取最大值,此时S四边形ABCD取得最大值,
将![]() 代入抛物线解析式可得:
代入抛物线解析式可得:![]()
此时点![]() 的坐标为
的坐标为![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某校为了解学生对排球、羽毛球、足球、篮球(以下分别用A、B、C、D表示)这四种球类运动的喜好情况.对全体学生进行了抽样调查(每位学生只能选一项最喜欢的运动),并将调查情况绘制成如下两幅不完整的统计图.
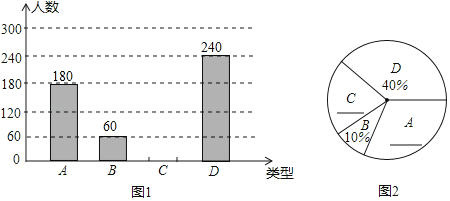
请根据以上信息回答下面问题:
(1)本次参加抽样调查的学生有 人.
(2)补全两幅统计图.
(3)若从本次参加抽样调查的学生中任取1人,则此人喜欢哪类球的概率最大?求其概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
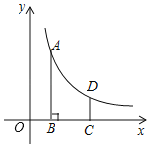
【题目】如图,反比例函数y=![]() (x>0)的图象上一点A(m,4),过点A作AB⊥x轴于B,CD∥AB,交x轴于C,交反比例函数图象于D,BC=2,CD=
(x>0)的图象上一点A(m,4),过点A作AB⊥x轴于B,CD∥AB,交x轴于C,交反比例函数图象于D,BC=2,CD=![]() .
.
(1)求反比例函数的表达式;
(2)若点P是y轴上一动点,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
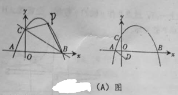
【题目】请从以下(A)、(B)两题中任选一个解答.
(A)已知:抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)抛物线的解析式为_____________;
(2)点![]() 为第一象限抛物线上一点,是否存在使
为第一象限抛物线上一点,是否存在使![]() 面积最大的点
面积最大的点![]() ?若不存在,请说明理由,若存在,求出点
?若不存在,请说明理由,若存在,求出点![]() 的坐标;
的坐标;
(3)点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() 将线段
将线段![]() 绕平面内某一点旋转
绕平面内某一点旋转![]() 得线段
得线段![]() (点
(点![]() 分别与点
分别与点![]() 对应),使点
对应),使点![]() 都在抛物线上,请直接写点
都在抛物线上,请直接写点![]() 的坐标.
的坐标.
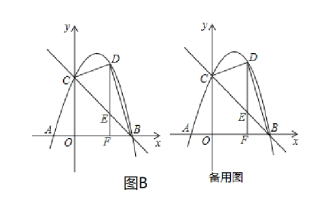
(B)如图,已知抛物线![]() 与
与![]() 轴从左至右交于
轴从左至右交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)抛物线的解析式为___________:
(2)![]() 是第一象限内抛物线上的一个动点(与点
是第一象限内抛物线上的一个动点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() ,直线
,直线![]() 能否把
能否把![]() 分成面积之比为
分成面积之比为![]() 的两部分?若能,请求出点
的两部分?若能,请求出点![]() 的坐标;若不能,请说明理由;
的坐标;若不能,请说明理由;
(3)若![]() 为抛物线对称轴上一动点,
为抛物线对称轴上一动点,![]() 为直角三角形,请直接写出点
为直角三角形,请直接写出点![]() 的坐标.
的坐标.
我选做的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
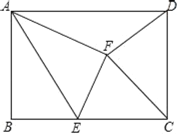
【题目】如图,在矩形ABCD中,点E是BC边上的一个动点,沿着AE翻折矩形,使点B落在点F处若AB=3,BC=![]() AB,解答下列问题:
AB,解答下列问题:
(1)在点E从点B运动到点C的过程中,求点F运动的路径长;
(2)当点E是BC的中点时,试判断FC与AE的位置关系,并说明你的理由;
(3)当点F在矩形ABCD内部且DF=CD时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
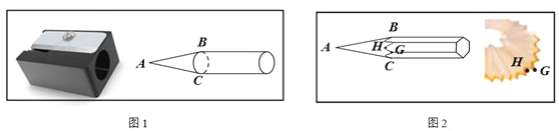
【题目】已知如图1,圆柱体铅笔插入卷笔刀充分卷削,得到底面直径BC为2的圆锥,∠BAC=30°.底面边长为1的正六棱柱铅笔插入卷削,得到如图2所示铅笔和锯齿状木屑(木屑厚度忽略不计),木屑锯齿齿锋点G相邻凹陷最低点为H,则AG=________,GH=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
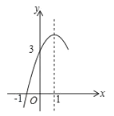
【题目】如图为抛物线的部分图象,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),下列结论:
①4ac<b2
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中正确的结论是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
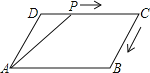
【题目】如图,在平行四边形ABCD中,∠DAB=60°,AB=5,BC=3,点P从点D出发,沿DC,CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与AD,AP所围成的图形的面积为y,y随x的变化而变化.在下列图象中,能正确反映y与x的函数关系的是( )
A.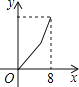 B.
B. C.
C.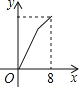 D.
D.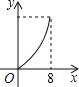
查看答案和解析>>
科目:初中数学 来源: 题型:
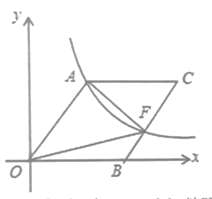
【题目】如图,在直角坐标系中,四边形OACB为菱形,OB在x轴的正半轴上,∠AOB=60°,过点A的反比例函数y= ![]() 的图像与BC交于点F,则△AOF的面积为 ______________.
的图像与BC交于点F,则△AOF的面积为 ______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com