
 如图,AB是⊙O的直径,点D是⊙O上一点,∠BAD的平分线交⊙O于点C,过点C的直线与AD互相垂直,垂足为点E,直线EC与AB的延长线交于点P,连接BC,已知PB:PC=1:$\sqrt{3}$.
如图,AB是⊙O的直径,点D是⊙O上一点,∠BAD的平分线交⊙O于点C,过点C的直线与AD互相垂直,垂足为点E,直线EC与AB的延长线交于点P,连接BC,已知PB:PC=1:$\sqrt{3}$.分析 (1)先判断出∠CAE=∠CAB,进而得出∠CAE=∠OCA,即可得出OC∥AE,即可得出结论;
(2)设出PB=x,则PC=$\sqrt{3}$x,先判断出△PBC∽△PCA,即可得出比例式即可得出PA=3x,即可得出结论;
(3)利用锐角三角函数求出∠BAC=30°,即可求出∠ABD=30°,即可求出AD,即可得出结论.
解答 解:(1)如图1,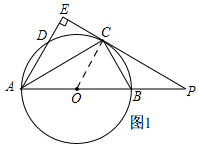 连接OC,
连接OC,
∴OA=OC,
∴∠OAC=∠OCA,
∵AC是∠BAD的平分线,
∴∠CAE=∠CAB,
∴∠CAE=∠OCA,
∴OC∥AE,
∵PC⊥AE,
∴PC⊥OC,
∵点C在⊙O上,
∴PC是⊙O的切线;
(2)PB=r,
理由:由(1)知,PC是⊙O的切线,
∴∠PCB=∠PAC,
∵∠A=∠A,
∴△PBC∽△PCA,
∴$\frac{PB}{PC}=\frac{PC}{PA}$=$\frac{BC}{AC}$,
设PB=x,则PC=$\sqrt{3}$x,
∴$\frac{x}{\sqrt{3}x}=\frac{\sqrt{3}x}{PA}$,
∴PA=3x,
∴PA=PB+AB=x+2r=3x,
∴r=x,
∴PB=r,
(3)如图2,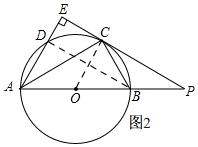
连接OC,
由(1)知,OC⊥PC,
由(2)知,BP=r=OB,
∴BC=$\frac{1}{2}$OP=r,
AC=$\sqrt{3}$BC=$\sqrt{3}$r=3$\sqrt{3}$,
在Rt△ABC中,sin∠BAC=$\frac{BC}{AB}$=$\frac{r}{2r}$=$\frac{1}{2}$,
∴∠BAC=30°,
∴∠BAD=2∠BAC=60°,
连接BD,
∴∠ADB=90°,
∴∠ABD=30°,
∴AD=$\frac{1}{2}$AB=r=3.
在Rt△ACE中,∠ACE=30°,cos∠CAE=$\frac{AE}{AC}$=$\frac{AE}{3\sqrt{3}}$,
∴AE=3$\sqrt{3}$×cos30°=$\frac{9}{2}$,
∴DE=AE-AD=$\frac{9}{2}$-3=$\frac{3}{2}$.
点评 此题是圆的综合题,主要考查了角平分线定理,切线的判定和性质,相似三角形的判定和性质,勾股定理,锐角三角函数,解(1)的关键是判断出OC∥AE,解(2)的关键是表示出PA,解(3)的关键是求出∠BAC=30°,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2017}}{{2}^{2016}}$ | B. | -$\frac{\sqrt{2017}}{{2}^{2016}}$ | C. | $\frac{\sqrt{2018}}{{2}^{2017}}$ | D. | -$\frac{\sqrt{2018}}{{2}^{2017}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
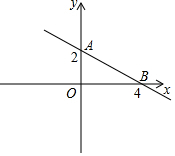 如图,直线AB与x轴,y轴的交点为A,B两点,点A,B的纵坐标、横坐标如图所示.问题:
如图,直线AB与x轴,y轴的交点为A,B两点,点A,B的纵坐标、横坐标如图所示.问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
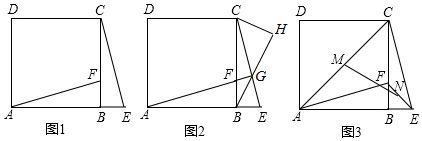
 如图,在△ABC中,∠C=90°,AE平分∠A交BC于E,CD⊥AB于D,交AE于F,FM∥AB交BC于M,求证(1)$\frac{AE}{AF}=\frac{AB}{AC}$;(2)$\frac{EB}{MB}=\frac{AE}{AF}$;(3)CE=BM.
如图,在△ABC中,∠C=90°,AE平分∠A交BC于E,CD⊥AB于D,交AE于F,FM∥AB交BC于M,求证(1)$\frac{AE}{AF}=\frac{AB}{AC}$;(2)$\frac{EB}{MB}=\frac{AE}{AF}$;(3)CE=BM.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 百分数都小于1 | |
| B. | 圆的周长是这个圆的半径的3.14倍 | |
| C. | 在含糖7%的糖水中,糖和水的比是7:100 | |
| D. | 如果两个扇形的圆心角相相等,那么半径越长所对的弧长也越长 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com