
| A. | $\frac{\sqrt{2017}}{{2}^{2016}}$ | B. | -$\frac{\sqrt{2017}}{{2}^{2016}}$ | C. | $\frac{\sqrt{2018}}{{2}^{2017}}$ | D. | -$\frac{\sqrt{2018}}{{2}^{2017}}$ |
分析 根据所给算式找出规律,即可解答.
解答 解:-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2+1}}{{2}^{2}}$,$\frac{\sqrt{2+2}}{{2}^{3}}$,-$\frac{\sqrt{2+3}}{{2}^{4}}$,-$\frac{\sqrt{2+4}}{{2}^{5}}$,-$\frac{\sqrt{2+5}}{{2}^{6}}$,则第2017个数是-$\frac{\sqrt{2+2016}}{{2}^{2017}}$=-$\frac{\sqrt{2018}}{{2}^{2017}}$.
故选:D.
点评 本题考查了算式平方根,解决本题的关键是熟记算式平方根的定义.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:选择题
| A. | (1-10%)a元 | B. | (1+10%)a元 | C. | $\frac{a}{1+10%}$元 | D. | $\frac{a}{1-10%}$元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
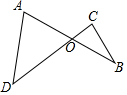 阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C,那么△AOD与△COB全等吗?若全等,试写出证明过程,若不全等,请说明理由
阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C,那么△AOD与△COB全等吗?若全等,试写出证明过程,若不全等,请说明理由查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
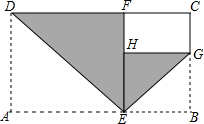 如图,长方形纸片ABCD,AB=a,BC=b,且b<a<2b,则∠ADC的平分线DE折叠纸片,点A落在CD边上的点F处,再沿∠BEF的平分线EG折叠纸片,点B落在EF边上的点H处.
如图,长方形纸片ABCD,AB=a,BC=b,且b<a<2b,则∠ADC的平分线DE折叠纸片,点A落在CD边上的点F处,再沿∠BEF的平分线EG折叠纸片,点B落在EF边上的点H处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,点D是⊙O上一点,∠BAD的平分线交⊙O于点C,过点C的直线与AD互相垂直,垂足为点E,直线EC与AB的延长线交于点P,连接BC,已知PB:PC=1:$\sqrt{3}$.
如图,AB是⊙O的直径,点D是⊙O上一点,∠BAD的平分线交⊙O于点C,过点C的直线与AD互相垂直,垂足为点E,直线EC与AB的延长线交于点P,连接BC,已知PB:PC=1:$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com