
【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D,F分别在边AC,BC上,易证:AD=BF(不需要证明);
(1)探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD,BF,其他条件不变,如图②,求证:AD=BF;
(2)应用:若α=45°,CD= ![]() ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= .
【答案】
(1)
证明:如图②,
∵四边形CDEF为正方形,
∴CD=CF,
由旋转得:∠ACD=∠BCF,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,
∴△ADC≌△BFC,
∴AD=BF;
(2)![]()
【解析】应用:如图③,∵四边形CDEF为正方形,
∴∠EDC=90°,ED=DC,
∵DC= ![]() ,
,
∴EC= ![]() =
= ![]() =2,
=2,
∴BC=BE+EC=1+2=3,
∴AC=BC=3,
过D作DG⊥AC于G,
∵α=45°,
即∠ACD=45°,
∴△DCG是等腰直角三角形,
∴DG=CG=1,
∴AG=BC﹣CG=3﹣1=2,
由勾股定理得:AD= ![]() =
= ![]() =
= ![]() ,
,
同理得:△ADC≌△BFC,
∴BF=AD= ![]() .
.
【考点精析】通过灵活运用等腰直角三角形和勾股定理的概念,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(﹣1,0),C(0,3)
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在P点,使△PCD是以CD为腰的等腰三角形,如果存在,直接写出点P的坐标,如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,
①求直线BC 的解析式;
②当点E运动到什么位置时,四边形CDBF的面积最大?求四边形CDBF的最大面积及此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某抛物线的对称轴为直线x=2,点E是该抛物线顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D,点A是对称轴上一点,连结AC,AB,若△ABC是等边三角形,则图中阴影部分图形的面积之和是 . 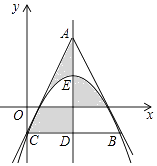
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
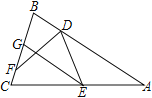
【题目】如图,在△ABC中,AB=AC,D、E分别为AB、AC上的点,∠BDE、∠CED的平分线分别交BC于点F、G,EG∥AB.若∠BGE=110°,则∠BDF的度数为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F,
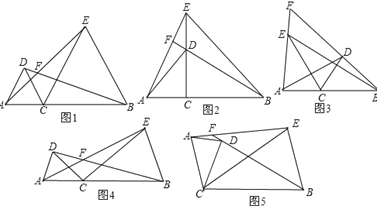
(1)如图1,若∠ACD=60°,则∠AFB= ;如图2,若∠ACD=90°,则∠AFB= ;如图3,若∠ACD=120°,则∠AFB= ;
(2)如图4,若∠ACD=α,则∠AFB= (用含α的式子表示);
(3)将图4中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),变成如图5所示的情形,若∠ACD=α,则∠AFB与α的有何数量关系?并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A,B,O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为 . 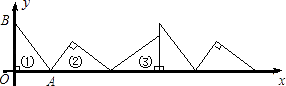
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于下列各组条件,不能判定△![]() ≌△
≌△![]() 的一组是 ( )
的一组是 ( )
A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com