
 如图,在矩形纸片ABCD中,AB<BC.点M、N分别在边AD、BC上,沿直线MN将四边形DMNC翻折,点C恰好与点A重合.如果此时在原图中△CDM与△MNC的面积比是1:3,那么$\frac{MN}{DM}$的值等于$2\sqrt{3}$.
如图,在矩形纸片ABCD中,AB<BC.点M、N分别在边AD、BC上,沿直线MN将四边形DMNC翻折,点C恰好与点A重合.如果此时在原图中△CDM与△MNC的面积比是1:3,那么$\frac{MN}{DM}$的值等于$2\sqrt{3}$. 分析 由折叠的性质可得:∠AMN=∠CMN,由四边形ABCD是矩形,可得∠AMN=∠CNM,则可证得∠CNM=∠CMN,继而可得CM=CN;过点M作MH⊥BC于点H,由△CDM的面积与△MNC的面积比为1:3,易得NC=3MD=3HC,然后设DM=x,由勾股定理,可求得MN的长,继而求得答案.
解答 解:由折叠的性质可得:∠EMN=∠DMN,
即∠EMN=∠EMA+∠AMN,
∠DMN=∠DMC+∠CMN,
∵∠EMA=∠DMC
∴∠AMN=∠CMN,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AMN=∠CNM,
∴∠CNM=∠CMN,
∴CM=CN,
如图,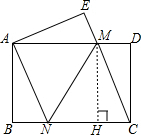
过点M作MH⊥BC于点H,则四边形MHCD是矩形,
∴HC=DM,MH=DC,
∵△CDM的面积与△CMN的面积比为1:3,
∴$\frac{{S}_{△CDM}}{{S}_{△CMN}}$=$\frac{\frac{1}{2}DM•MH}{\frac{1}{2}CN•NH}=\frac{DM}{CN}=\frac{1}{3}$,
∴NC=3MD=3HC,
∴NH=2HC,
设DM=x,则HC=x,NH=2x,
∴CM=CN=3x,
在Rt△CDM中,DC=$\sqrt{C{M}^{2}-D{M}^{2}}$=2$\sqrt{2}$x,
∴HM=2$\sqrt{2}$x,
在Rt△MNH中,MN=$\sqrt{M{H}^{2}+N{H}^{2}}$=2$\sqrt{3}$x,
∴$\frac{MN}{DM}=\frac{2\sqrt{3}x}{x}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 此题考查了矩形的性质、折叠的性质、勾股定理以及三角形的面积.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源:2016-2017学年四川达县万家中学下学期九年级第一次月考数学试卷(解析版) 题型:解答题
五•一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.下图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题:
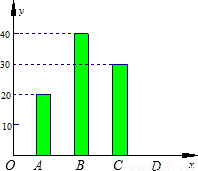
(1)若去D地的车票占全部车票的10%,请求出D地车票的数量,并补全统计图;
(2)若公司采用随机抽取的方式分发车票,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小胡抽到去A地的概率是多少?
(3)若有一张车票,小王、小李都想要,决定采取抛掷一枚各面分别标有1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小王掷得着地一面的数字比小李掷得着地一面的数字小,车票给小王,否则给小李”.试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:单选题
观察图中菱形四个顶点所标的数字规律,可知数2017应标在( )
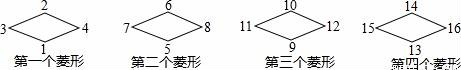
A. 第504个菱形的左边 B. 第505个菱形的下边
C. 第504个菱形的上边 D. 第505个菱形的右边
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
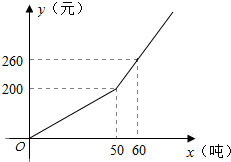 已知某市2014年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2014年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (-1,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com