Question

（1）已知△ABC中，∠A=90°，∠B=67.5°，请画一条直线，把这个三角形分割成两个等腰三角形．（请你选用下面给出的备用图，把所有不同的分割方法都画出来．只需画图，不必说明理由，但要在图中标出相等两角的度数）

（2）已知△ABC中，∠C是其最小的内角，过顶点B的一条直线把这个三角形分割成了两个等腰三角形，请探求∠ABC与∠C之间的关系．

Answer 1

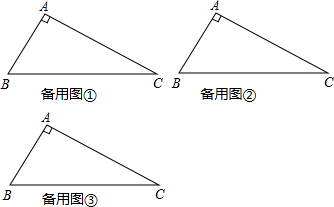
解：（1）如图（共有2种不同的分割法）．


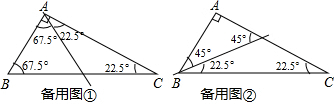
（2）设∠ABC=y，∠C=x，过点B的直线交边AC于D．在△DBC中，
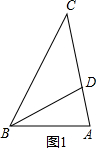
①若∠C是顶角，如图1，则∠ADB＜90°，∠CBD=∠C=（180°-x）=90°-x，∠A=180°-x-y．
此时只能有∠A=∠ABD，即180°-x-y=y-（90°-x），
∴3x+4y=540°，即∠ABC=135°-∠C．

②若∠C是底角，
第一种情况：如图2，当DB=DC时，则∠DBC=x，△ABD中，∠ADB=2x，∠ABD=y-x．
由AB=AD，得2x=y-x，此时有y=3x，即∠ABC=3∠C．
由AB=BD，得180°-x-y=2x，此时3x+y=180°，即∠ABC=180°-3∠C．
由AD=BD，得180°-x-y=y-x，此时y=90°，即∠ABC=90°，∠C为小于45°的任意锐角．
第二种情况，如图3，当BD=BC时，∠BDC=x，∠ADB=180°-x＞90°，此时只能有AD=BD，
从而∠A=∠ABD=∠C＜∠C，这与题设∠C是最小角矛盾．
∴当∠C是底角时，BD=BC不成立．
综上，∠ABC与∠C之间的关系是：∠ABC=135°-∠C．
或∠ABC=3∠C．
分析：（1）已知角度，要分割成两个等腰三角形，可以运用直角三角形、等腰三角形性质结合三角形内角和定理，先计算出可能的角度，或者先从草图中确认可能的情况，及角度，然后画上．
（2）在（1）的基础上，由“特殊”到“一般”，需要把直角三角形分成两个等腰三角形的各种情形列方程，可得出角与角之间的关系．
点评：本题考查了等腰三角形的性质；第（1）问是计算与作图相结合的探索．本问对学生运用作图工具的能力，以及运用直角三角形、等腰三角形性质等基础知识解决问题的能力都有较高的要求．
第（2）问在第（1）问的基础上，由“特殊”到“一般”，“分类讨论”把直角三角形分成两个等腰三角形的各种情形并结合“方程思想”探究角与角之间的关系．本题不仅趣味性强，创造性强，而且渗透了由“特殊”到“一般”、“分类讨论”、“方程思想”、“转化思想”等数学思想，是一道不可多得的好题．