
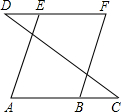
 已知:DF∥AC,∠A=∠F.求证:AE∥BF.
已知:DF∥AC,∠A=∠F.求证:AE∥BF. 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
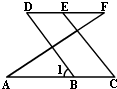 21、在下面解答过程的横线上填空.
21、在下面解答过程的横线上填空.查看答案和解析>>
科目:初中数学 来源: 题型:
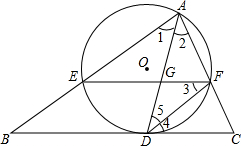 如图,△ABC中,∠BAC的平分线AD交BC于D,⊙O过点A,且和BC切于D,和AB、AC分别交于E、F.设EF交AD于G,连接DF.
如图,△ABC中,∠BAC的平分线AD交BC于D,⊙O过点A,且和BC切于D,和AB、AC分别交于E、F.设EF交AD于G,连接DF.| AE | EB |
查看答案和解析>>
科目:初中数学 来源:数学测试卷 七年级下册 题型:022
已知:DF∥AC,∠A=∠F,求证:AE∥BF.
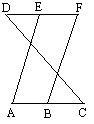
证明:∵DF∥AC(已知),
∴∠FBC=∠________( ).
∵∠A=∠F(已知),
∴∠A=∠FBC( ).
∴AE∥FB( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com