
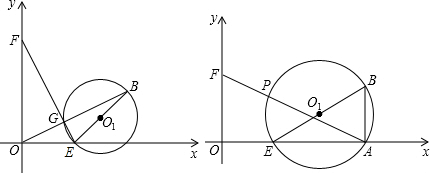
分析 (1)要判断点G与⊙O1的位置关系,只需比较O1G与⊙O1的半径O1B的大小.设点E出发t秒,则E(t,0),F(0,2t),用待定系数法求出直线EF和直线OB的解析式,确定点G的坐标,用两点间的距离公式计算出O1G与O1B的大小,从而进行判定;
(2)如果t秒时FB与⊙O1相切,那么∠FBE=90°;在RT△BEF与RT△OEF中,根据EF不变列出方程,求出t的值;
(3)设点F出发t秒,则E(t+2,0),F(0,2t);设P(x,y),由tan∠FAO=y:(4-x)=2t:4,得出x=4-$\frac{2}{t}$y,即P(4-$\frac{2}{t}y$,y);因为BE为直径,所以∠BPE=90°,PE2+BP2=BE2,得出y与t的关系,可以含t的代数式得出P的坐标,分别计算AP,AF的长,根据结果判断.
解答 解:(1)连接O1G,
设点E出发t秒,则E(t,0),F(0,2t),
设直线EF的方程为y=kx+b,则$\left\{\begin{array}{l}{kt+b=0}\\{b=2t}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=2t}\end{array}\right.$,
∴y=-2x+2t,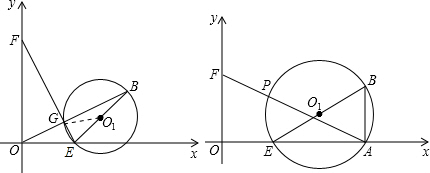
∴直线OB的方程为y=$\frac{1}{2}$x;
∵解方程组$\left\{\begin{array}{l}{y=-2x+2t}\\{y=\frac{1}{2}x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{4}{5}t}\\{y=\frac{2}{5}t}\end{array}\right.$,
∴G($\frac{4}{5}$t,$\frac{2}{5}$t);
∵O1是BE的中点,
∴O1($\frac{4+t}{2}$,1),
∴O1G2=($\frac{4+t}{2}$-$\frac{4}{5}$t)2+(1-$\frac{2}{5}$t)2=$\frac{1}{4}$t2-2t+5,O1B2=(4-$\frac{4+t}{2}$)2+12=$\frac{1}{4}$t2-2t+5,
∴O1G=O1B,点G在⊙O1上;
(2)设t秒时FB与⊙O1相切,那么E(t,0),F(0,2t),∠FBE=90°,
∵EF2=BE2+BF2,EF2=OE2+OF2,
∴(4-t)2+22+42+(2-2t)2=t2+(2t)2,
解得t=2.5;
(3)设点F出发t秒,则E(t+2,0),F(0,2t),
设P(x,y),
∵tan∠FAO=y:(4-x)=2t:4,
∴x=4-$\frac{2}{t}$y,
∴P(4-$\frac{2}{t}$y,y),
∵BE为直径,
∴∠BPE=90°,
∵PE2+BP2=BE2,
∴利用两点间的距离公式把B、P、E、F各点的坐标代入得,
∴y=$\frac{4t}{{t}^{2}+4}$,
∴x=$\frac{{4t}^{2}+8}{{t}^{2}+4}$,
即P($\frac{{4t}^{2}+8}{{t}^{2}+4}$,$\frac{4t}{{t}^{2}+4}$),
∴AP2=(4-$\frac{{4t}^{2}+8}{{t}^{2}+4}$)2+($\frac{4t}{{t}^{2}+4}$)2,
∴AP=$\frac{4}{{t}^{2}+4}$×$\sqrt{{t}^{2}+4}$,AF=$\sqrt{16+{4t}^{2}}$=2$\sqrt{{t}^{2}+4}$,
∴AP•AF=8,是不会发生变化的.
点评 本题综合考查了切线的判定,三角函数等知识,善于抓住不变量,找到等量关系是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把边长为2的正方形剪成四个完全一样的直角三角形,在下面对应的正方形网格(每个小正方形的边长均为1)中画出用这四个直角三角形按要求分别拼成的新的多边形.(要求全部用上,互不重叠,互不留隙).
如图,把边长为2的正方形剪成四个完全一样的直角三角形,在下面对应的正方形网格(每个小正方形的边长均为1)中画出用这四个直角三角形按要求分别拼成的新的多边形.(要求全部用上,互不重叠,互不留隙).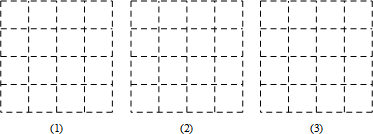
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
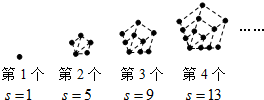
| A. | 29 | B. | 25 | C. | 24 | D. | 22 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com