
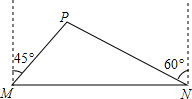
 我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 分析 根据题意,在△MNP中,∠MNP=30°,∠PMN=45°,MN=2千米,是否搬迁看P点到MN的距离与0.6的大小关系,若距离大于0.6千米则不需搬迁,反之则需搬迁,因此求P点到MN的距离,作PD⊥MN于D点.
解答 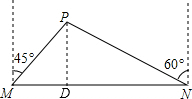 解:过点P作PD⊥MN于D
解:过点P作PD⊥MN于D
∴MD=PD•cot45°=PD,
ND=PD•cot30°=$\sqrt{3}$PD,
∵MD+ND=MN=2,
即$\sqrt{3}$PD+PD=2,
∴PD=$\frac{2}{\sqrt{3}+1}$=$\sqrt{3}$-1≈1.73-1=0.73>0.6.
答:修的公路不会穿越住宅小区,故该小区居民不需搬迁.
点评 考查了解直角三角形的应用-方向角问题,“化斜为直”是解三角形的基本思路,常需作垂线(高),原则上不破坏特殊角(30°、45°、60°).


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
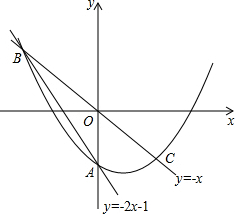 在平面直角坐标系中,O为原点,直线y=-2x-1与y轴交于点A,与直线y=-x交于点B,点B关于原点的对称点为点C.
在平面直角坐标系中,O为原点,直线y=-2x-1与y轴交于点A,与直线y=-x交于点B,点B关于原点的对称点为点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | y1=-y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2500x2=3500 | B. | 2500(1+x)2=3500 | ||
| C. | 2500(1+x%)2=3500 | D. | 2500(1+x)+2500(1+x)2=3500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com