

分析 (1)由三角函数得出$\frac{AC}{AB}$=$\frac{3}{2}$,设AB=2x,则AC=3x,由勾股定理得出方程,解方程求出AE、AC,再证明△CDE∽△BAC,得出比例式求出CD,根据勾股定理求出AD即可;
(2)①由平行线得出比例式,证出MN∥BC,得出内错角相等,即可得出结论;
②由平行线得出比例式,得出MN=$\frac{BC•CE}{BC+CE}$=$\frac{BC•CE}{10}$,再由BC=CE=5时,BC•CE最大,即可得出结果.
解答 (1)解:∵BC=2CE,CE=1,
∴BE=2,
∵△ABC是直角三角形,
∴∠BAC=90°,
∵tan∠B=$\frac{AC}{AB}$,
∴$\frac{AC}{AB}$=$\frac{3}{2}$,
设AB=2x,则AC=3x,
根据勾股定理得:AB2+AC2=BC2,
∴(2x)2+(3x)2=22,
解得:x=$\frac{2\sqrt{13}}{13}$,
∴AB=$\frac{4\sqrt{13}}{13}$,AC=$\frac{6\sqrt{13}}{13}$,
∵∠ACB=∠DEC,
∴AC∥DE,
∴∠ACD=∠CDE=90°,
∵∠BAC=∠CDE=90°,
∴△CDE∽△BAC,
∴$\frac{CD}{AB}=\frac{CE}{BC}$=$\frac{DE}{AC}$=$\frac{1}{2}$,∠DCE=∠ABC,
∴CD=$\frac{1}{2}$AB=$\frac{2\sqrt{13}}{13}$,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{(\frac{6\sqrt{13}}{13})^{2}+(\frac{2\sqrt{13}}{13})^{2}}$=$\frac{2\sqrt{130}}{13}$;
(2)①证明:∵AC∥DE,
∴$\frac{DN}{CN}=\frac{DE}{AC}$,
∵∠BAC=∠ACD=90°,
∴AB∥CD,
∴$\frac{CD}{AB}=\frac{DM}{BM}$,
∴$\frac{DN}{CN}=\frac{DM}{BM}$,
∴MN∥BC,
∴∠CNM=∠DCE,
∴∠CNM=∠ABC;
②解:∵MN∥BC,AC∥DE,
∴$\frac{MN}{BC}=\frac{DN}{CD}$=$\frac{NE}{AE}=\frac{CE}{BE}$,$\frac{MN}{CE}=\frac{AN}{AE}=\frac{BC}{BE}$,
∴$\frac{MN}{BC}+\frac{MN}{CE}$=$\frac{CE}{BE}+\frac{BC}{BE}$=1,
∴MN=$\frac{BC•CE}{BC+CE}$=$\frac{BC•CE}{10}$,
∵BC+CE=10,
∴BC=CE=5时,BC•CE最大=25,
∴MN的最大值=2.5.
故答案为:2.5.
点评 本题是相似形综合题目,考查了相似三角形的判定与性质、平行线的判定与性质、勾股定理、三角函数、直角三角形的性质、解方程等知识;本题难度较大,综合性强,需要证明三角形相似和多次运用平行线得出比例式才能得出结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 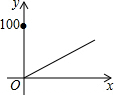 | B. | 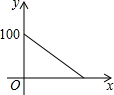 | C. | 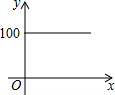 | D. | 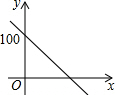 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
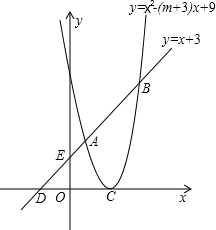 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴交于D、E两点.
如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴交于D、E两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
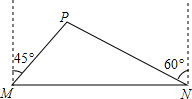 我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
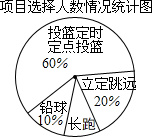 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com