
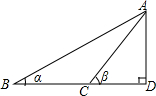
 如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )
如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )| A. | $\frac{tanα•tanβ}{tanβ-tanα}$•a | B. | ($\frac{1}{tanα}$-$\frac{1}{tanβ}$)•a | ||
| C. | $\frac{1}{tanα-tanβ}$•a | D. | (tanα-tanβ)•a |
科目:初中数学 来源: 题型:解答题
| 次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 |
| 运动升降 | -1200 | -20 | 30 | 20 | 60 | -80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
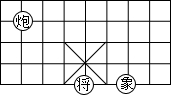 如图,象棋棋盘上.若“将“位于点(1,-2)“象“位于点(3,-2),则“炮“位于点( )
如图,象棋棋盘上.若“将“位于点(1,-2)“象“位于点(3,-2),则“炮“位于点( )| A. | (-1,1) | B. | (-1,2) | C. | (-2,1) | D. | (-2,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
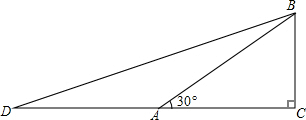 若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?
若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com