
【题目】例1:在等腰三角形ABC,∠A=120°,求B的度数.
例2:在等腰三角形ABC中,∠A=50°,求∠B的度数.
王老师启发同学们进行变式,小兰编了如下一题:变式等腰三角形ABC中,∠A=70°,求∠B的度数;
(1)请你解答小兰的变式题;
(2)解完(1)后,小兰发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°;
①当∠B的度数唯一时请你探索x的取值范围并用含x的式子表示∠B的度数;
②当∠B有三个不同的度数时请你探索x的取值范围,并用含x的式子表示∠B的度数.
【答案】(1)∠B=55°或40°或70°;(2)①∠B=90°﹣![]() x°(90°≤x<180°);②当0<x<90且x≠60时,∠B有三个不同的度数.∠B=(
x°(90°≤x<180°);②当0<x<90且x≠60时,∠B有三个不同的度数.∠B=(![]() )°;∠B=(180﹣2x)°;∠B=x°.
)°;∠B=(180﹣2x)°;∠B=x°.
【解析】
(1)由于等腰三角形的顶角和底角没有明确,因此要分类讨论;
(2)①当90≤x<180时,∠A只能为顶角,∠B的度数只有一个,根据三角形的内角和即可得到结论;
②分两种情况:当90≤x<180;当0<x<90,结合三角形内角和定理求解即可.
(1)若∠A为顶角,则∠B=(180°﹣∠A)÷2=55°;
若∠A为底角,∠B为顶角,则∠B=180°﹣2×70°=40°;
若∠A为底角,∠B为底角,则∠B=70°;
故∠B=55°或40°或70°;
(2)①当90≤x<180时,∠A只能为顶角,
∴∠B的度数只有一个,
∴∠B=![]() (180°﹣x°)=90°﹣
(180°﹣x°)=90°﹣![]() x°(90°≤x<180°);
x°(90°≤x<180°);
②分两种情况:当90≤x<180时,∠A只能为顶角,
∴∠B的度数只有一个,
当0<x<90时,
若∠A为顶角,则∠B=(![]() )°;
)°;
若∠A为底角,∠B为顶角,则∠B=(180﹣2x)°;
若∠A为底角,∠B为底角,则∠B=x°.
当![]() ≠180﹣2x且180﹣2x≠x且
≠180﹣2x且180﹣2x≠x且![]() ≠x,
≠x,
即x≠60时,∠B有三个不同的度数.
综上所述,可知当0<x<90且x≠60时,∠B有三个不同的度数.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
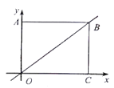
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 分别在坐标轴的正半轴上,
分别在坐标轴的正半轴上, ![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与折线
与折线![]() 有公共点.
有公共点.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)对于一次函数![]() ,当
,当![]() 随
随![]() 的增大而减小时,直接写出
的增大而减小时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图反映了我国五年来农村贫困人口的相关情况,其中“贫困发生率”是指贫困人口占目标调查人口的百分比.
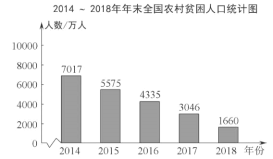
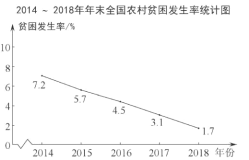
(以上数据来自国家统计局)
根据统计图提供的信息,下列推断不合理的是( )
A. 与2017年相比,2018年年末全国农村贫困人口减少了1386万人
B. 2015~2018年年末,与上一年相比,全国农村贫困发生率逐年下降
C. 2015~2018年年末,与上一年相比,全国农村贫困人口的减少量均超过1000万
D. 2015~2018年年末,与上一年相比,全国农村贫困发生率均下降1.4个百分点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察猜想
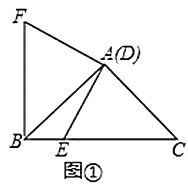
(1)如图①,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 与点
与点![]() 重合,点
重合,点![]() 在边
在边![]() 上,连接
上,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,连接
,连接![]() ,
,![]() 与
与![]() 的位置关系是________,
的位置关系是________,![]() ________;
________;
探究证明
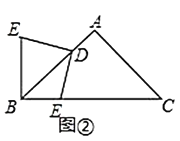
(2)在(1)中,如果将点![]() 沿射线
沿射线![]() 方向移动,使
方向移动,使![]() ,其余条件不变,如图②判断
,其余条件不变,如图②判断![]() 与
与![]() 的位置关系,并求
的位置关系,并求![]() 的值,请写出你的理由或计算过程;
的值,请写出你的理由或计算过程;
拓展延伸
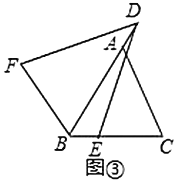
(3)如图③,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转,旋转角
顺时针旋转,旋转角![]() ,连接
,连接![]() ,则
,则![]() 的值是多少?请用含有
的值是多少?请用含有![]() ,
,![]() 的式子直接写出结论.
的式子直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),给出以下五个结论:①AE=CF;②∠APE=∠CPF;③连接EF,△EPF是等腰直角三角形;④EF=AP;⑤S四边形AFPE=S△APC,其中正确的有几个( )
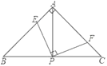
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的边AB=6,BC=12,点P为矩形ABCD边上一点,连接AP,若线段AP、BD交点为点H,△PAB为等腰三角形,则AH的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
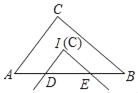
【题目】如图,点I是Rt△ABC的内心,∠C=90°,AC=3,BC=4,将∠ACB平移使其顶点C与I重合,两边分别交AB于D、E,则△IDE的周长为( )
A.3B.4C.5D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公路上有A、B、C三个汽车站,一辆汽车8:00从离A站10km的P地出发,向C站匀速行驶,15min后离A站30km.
(1)设出发x h后,汽车离A站y km,写出y与x之间的函数表达式;
(2)当汽车行驶到离A站250km的B站时,接到通知要在12:00前赶到离B站60km的C站.汽车按原速行驶,能否准时到达?如果能,那么汽车何时到达C站?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16.点D在边BC上,且点D到边AB和边AC的距离相等.
(1)用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上标注出点D);
(2)求点D到边AB的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com