
【题目】矩形ABCD的边AB=6,BC=12,点P为矩形ABCD边上一点,连接AP,若线段AP、BD交点为点H,△PAB为等腰三角形,则AH的长为____.
【答案】![]() 或
或![]()
【解析】
根据题意画出图形,分两种情况:①当P在BC上时;AB=BP,②当P在CD上时,P为CD的中点,PA=PB,由矩形的性质和勾股定理以及相似三角形的性质即可得出结果.
分两种情况:
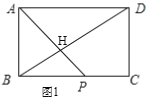
①如图1,当P在BC上时,
∵四边形ABCD是矩形,
∴AD=BC=12,AD//BC,∠ABP=90°,
∴△ADH∽△PBH,
∴![]() ,
,
∵△PAB为等腰三角形,∠ABP=90°,
∴AB=PB=6,AP=6![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:AH=4![]() ,
,
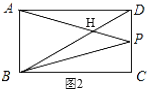
②如图2,当P在CD上时,PA=PB,
∴P为CD的中点,
∴PD=![]() CD=3,
CD=3,
∴AP=![]() =
=![]() =3
=3![]() ,
,
∵AB//CD,
∴△ABH∽△PDH,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:AH=2![]() .
.
综上所述:AH的长为4![]() 或2
或2![]() .
.
故答案为:4![]() 或2
或2![]()


科目:初中数学 来源: 题型:
【题目】某工程队承接了60万平方米的绿化工程,由于情况有变,……设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A. 实际工作时每天的工作效率比原计划提高了![]() 结果提前30天完成了这一任务
结果提前30天完成了这一任务
B. 实际工作时每天的工作效率比原计划提高了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
C. 实际工作时每天的工作效率比原计划降低了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
D. 实际工作时每天的工作效率比原计划降低了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,与y轴交于点B,与抛物线
,与y轴交于点B,与抛物线![]() 的对称轴交于点
的对称轴交于点![]() .
.
(1)求m的值;
(2)求抛物线的顶点坐标;
(3)![]() 是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点
是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点![]() ,
,![]() (点P在点Q的左侧).若
(点P在点Q的左侧).若![]() 恒成立,结合函数的图象,求a的取值范围.
恒成立,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B,E是半圆弧的三等分点,弧AB的长为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )

A. 6![]() ﹣
﹣![]() B. 9
B. 9![]() ﹣
﹣![]() C.
C. ![]() ﹣
﹣![]() D. 6
D. 6![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】例1:在等腰三角形ABC,∠A=120°,求B的度数.
例2:在等腰三角形ABC中,∠A=50°,求∠B的度数.
王老师启发同学们进行变式,小兰编了如下一题:变式等腰三角形ABC中,∠A=70°,求∠B的度数;
(1)请你解答小兰的变式题;
(2)解完(1)后,小兰发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°;
①当∠B的度数唯一时请你探索x的取值范围并用含x的式子表示∠B的度数;
②当∠B有三个不同的度数时请你探索x的取值范围,并用含x的式子表示∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
旋转是图形变化的方法之一,借助旋转知识可以解决线段长、角的大小、取值范围、判断三角形形状等问题,在实际生活中也有着十分重要的地位和作用.
问题背景
一块等边三角形建筑材料内一点到三角形三个顶点的距离满足一定条件时,我们可以用所学的知识帮助工人师傅在没有刻度尺的情况下求出等边三角形的边长.
数学建模
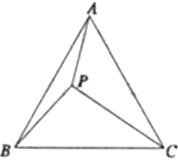
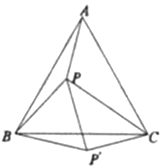
如图,等边三角形![]() 内有一点
内有一点![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
问题解决
(1)如图,将△ABP绕点![]() 顺时针旋转60°得到△CBP′,连接
顺时针旋转60°得到△CBP′,连接![]() ,易证∠BP′P=__°,△____为等边三角形,
,易证∠BP′P=__°,△____为等边三角形,![]() ____
____![]() ,
,![]() ___°.
___°.
(2)点H为直线BP′上的一个动点,则![]() 的最小值为______;
的最小值为______;
(3)求![]() 长;
长;
拓展延伸
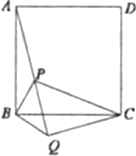
己知:点![]() 在正方形
在正方形![]() 内,点
内,点![]() 在平面内,
在平面内,![]() ,
,![]() .
.
(4)在图中,连接PA、PC、PQ、QC,![]() ,若点
,若点![]() 、
、![]() 、
、![]() 在一条直线上,则
在一条直线上,则![]() ____.
____.
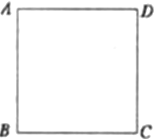
(5)若![]() ,连接
,连接![]() ,则______
,则______![]() ______;连接
______;连接![]() ,当
,当![]() 、
、![]() 、
、![]() 三点在同一条直线上时,△BDQ的面积为______.
三点在同一条直线上时,△BDQ的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36000元购进甲、乙两种商品,销售完后共获利6000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
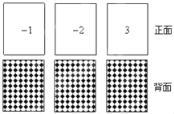
【题目】有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作二次函数表达式y=a(x﹣2)2+c中的a,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作表达式中的c.
(1)求抽出a使抛物线开口向上的概率;
(2)求抛物线y=a(x﹣2)2+c的顶点在第四象限的概率.(用树状图或列表法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
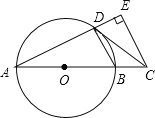
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=2![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
(3)在(2)的条件下,求弧BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com