
【题目】如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数. 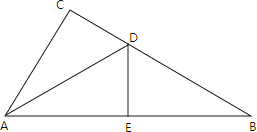
【答案】30°
解:∵DE垂直平分AB,∴∠DAE=∠B,∵在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,∴∠DAE=(90°-∠B)=∠B,∴3∠B=90°,∴∠B=30°.
【解析】根据DE垂直平分AB,求证∠DAE=∠B,再利用角平分线的性质和三角形内角和定理,即可求得∠B的度数.
【考点精析】利用三角形的内角和外角和角平分线的性质定理对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.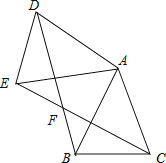
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( ) 
A.50°
B.51°
C.51.5°
D.52.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
A.点C
B.点D或点E
C.线段DE(异于端点) 上一点
D.线段CD(异于端点) 上一点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| AA′=BB′ | |
轴对称 |
| ||
旋转 |
| AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补. |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定位多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com