
 如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为$\frac{7}{4}$.
如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为$\frac{7}{4}$. 分析 根据矩形性质得AB=DC=6,BC=AD=8,AD∥BC,∠B=90°,再根据折叠性质得∠DAC=∠D′AC,而∠DAC=∠ACB,则∠D′AC=∠ACB,所以AE=EC,设BE=x,则EC=8-x,AE=8-x,然后在Rt△ABE中利用勾股定理可计算出BE的长即可.
解答 解:∵四边形ABCD为矩形,
∴AB=DC=6,BC=AD=8,AD∥BC,∠B=90°.
∵△ACD沿AC折叠到△ACD′,AD′与BC交于点E,
∴∠DAC=∠D′AC.
∵AD∥BC,
∴∠DAC=∠ACB.
∴∠D′AC=∠ACB.
∴AE=EC.
设BE=x,则EC=8-x,AE=8-x.
∵在Rt△ABE中,AB2+BE2=AE2,
∴62+x2=(8-x)2,解得x=$\frac{7}{4}$,即BE的长为$\frac{7}{4}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:选择题
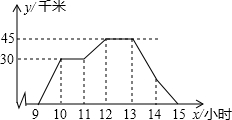 A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )
A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )
如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )| A. | $\frac{DE}{AE}$=$\frac{DF}{BF}$ | B. | $\frac{EF}{AB}$=$\frac{DF}{DB}$ | C. | $\frac{EF}{CD}$=$\frac{DF}{BF}$ | D. | $\frac{EF}{CD}$=$\frac{DF}{DB}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家,小亮和妈妈的行进路程S(km)与时间t(时)的函数图象如图所示,则下列说法中错误的有( )
小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家,小亮和妈妈的行进路程S(km)与时间t(时)的函数图象如图所示,则下列说法中错误的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 中国象棋是一个具有悠久历史的游戏.如图的棋盘上,可以把每个棋子看作是恰好在某个正方形顶点上的一个点,若棋子“帅”对应的数对(1,0 ),棋子“象”对应的数对(3,-2),则图中棋盘上“卒”对应的数对是(3,-1)).
中国象棋是一个具有悠久历史的游戏.如图的棋盘上,可以把每个棋子看作是恰好在某个正方形顶点上的一个点,若棋子“帅”对应的数对(1,0 ),棋子“象”对应的数对(3,-2),则图中棋盘上“卒”对应的数对是(3,-1)).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com