

分析 (1)将C点坐标代入抛物线解析式可求k的值,由抛物线解析式求A,B两点坐标;
(2)根据A、B、M、N四点坐标,将四边形分割为两个三角形和一个梯形求面积;
(3)只要使△DBC面积最大即可,由此求D点坐标;
解答 解:(1)将C(0,-3)代入抛物线y=x2-2x+k中,得k=-3,
∴抛物线解析式为y=x2-2x-3,
令y=0,得x=-1或3,
∴A(-1,0),B(3,0);
故答案为-3,(-1,0),(3,0);
(2)如图(1),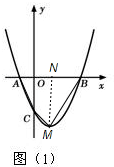
过M点作MN⊥AB,垂足为N,
由y=x2-2x-3=(x-1)2-4,可知M(1,-4),
∴S四边形ABMC=S△ACO+S梯形OCMN+S△BMN=$\frac{1}{2}$×1×3+$\frac{1}{2}$×(3+4)×1+$\frac{1}{2}$×(3-1)×4=9;
(3)存在,如图(2),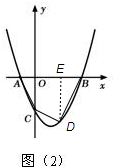
设D(m,m2-2m-3),
过D点作DE⊥AB,垂足为E,则
S四边形ABDC=S△ACO+S梯形OCDE+S△BDE
=$\frac{1}{2}$×1×3+$\frac{1}{2}$×[3-(m2-2m-3)]×m+$\frac{1}{2}$×(3-m)×[-(m2-2m-3)]
=-$\frac{3}{2}$m2+$\frac{9}{2}$m+6,
∵-$\frac{3}{2}$<0,
∴当m=-$\frac{\frac{9}{2}}{-3}$=$\frac{3}{2}$时,S四边形ABDC最大,此时D($\frac{3}{2}$,-$\frac{15}{4}$).
点评 本题考查了二次函数的综合运用.关键是根据题意求抛物线解析式,将四边形分割为三角形与梯形的面积和求解,同时考查了坐标系中,线段的垂直关系.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为$\frac{7}{4}$.
如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为$\frac{7}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “奔跑吧,兄弟”节目的收视率 | B. | “神州十一号”飞船的零件合格率 | ||
| C. | 某种品牌节能灯的使用寿命 | D. | 全国植树节中栽植树苗的成活率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x+1}{3}≥x-1}\end{array}\right.$,把解集表示在数轴上,并写出所有非负整数解.
解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x+1}{3}≥x-1}\end{array}\right.$,把解集表示在数轴上,并写出所有非负整数解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1.
如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 6台 | 7650元 |
| 第二周 | 4台 | 10台 | 11800元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC-CD-DE,如图所示,从甲队开始工作时计时.
甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC-CD-DE,如图所示,从甲队开始工作时计时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com