
����Ŀ��.ij�̳�Ϊ������ͣ����������,�⽨�����ͣ����,��ͼ�Ǹõ���ͣ�����µ���ڵ����ʾ��ͼ,����,AB��BD,��BAD=18��,C��BD��,BC=0.5 m.���ݹ涨,����ͣ�����µ�����Ϸ�Ҫ�����߱�־,�Ա��֪��ʻԱ���ݳ����ܷ�ȫʻ��.С����ΪCD�ij����������Ƶĸ߶�,��С����ΪӦ����CE�ij���Ϊ���Ƶĸ߶�.С����С��˭˵�ö�?�����жϲ��������ȷ�Ľ��.(�����ȷ��0.1 m,�ο�����:sin 18���0.31,cos 18���0.95,tan 18���0.325)
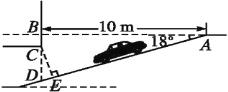
���𰸡�С��˵�ö�,CEΪ2.7m.
��������
�ȸ���CE��AE���жϳ�CEΪ�ߣ��ٸ��ݽ�ֱ�������ε�֪ʶ���
�⣺����ABD��,��ABD=90��,��BAD=18��,BA=10,
��tan��BAD=![]() ,��BD=10��tan18��.
,��BD=10��tan18��.
��CD=BD-BC=10��tan18��-0.5��2.8(m).
����ABD��,��CDE=90��-��BAD=72��.
��CE��ED,���DCE=18��.��cos��DCE=![]()
��CE=CD��cos��CDE=2.8��cos18���2.7(m).
��2.7m<2.8m,��CE��AE,��С��˵�ö�.
���,С��˵�ö�,CEΪ2.7m.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��B������ֱ�Ϊ��8��0������0��2![]() ����C��AB���е㣬����C��y��Ĵ��ߣ�����ΪD������P�ӵ�D��������DC���C�����˶�������P��x��Ĵ��ߣ�����ΪE������BP��EC����BP����ֱ����EC����ֱ�ߴ�ֱʱ����P������Ϊ____
����C��AB���е㣬����C��y��Ĵ��ߣ�����ΪD������P�ӵ�D��������DC���C�����˶�������P��x��Ĵ��ߣ�����ΪE������BP��EC����BP����ֱ����EC����ֱ�ߴ�ֱʱ����P������Ϊ____

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��

��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
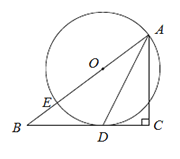
����Ŀ����֪����ͼ����Rt��ABC�У���C=90�㣬��E��б��AB�ϣ���AEΪֱ���ġ�O��BC�������ڵ�D������AD.
��1����֤��AD�ǡ�BAC��ƽ���ߣ�
��2����AC=3��BC=4�����O�İ뾶.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ�ĸ�����
��������ʽ![]() �����壬��x��ȡֵ��ΧΪx��1��x��0��
�����壬��x��ȡֵ��ΧΪx��1��x��0��
��������̬���γ����γɹ�ģ��2012��ȫ����̬��������Ϊ302 600 000Ԫ������������Ч�����ÿ�ѧ��������ʾΪ3.03��108Ԫ��
��������������![]() ��mΪ����������x��0ʱ��y��x�����������һ�κ���y=��2x+m��ͼ��һ����������һ���ޣ�
��mΪ����������x��0ʱ��y��x�����������һ�κ���y=��2x+m��ͼ��һ����������һ���ޣ�
����������ͼ�����y��Գƣ�������Ϊż��������������������y=3��y=2x+1��y=x2��ż�����ĸ���Ϊ2����
A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(����)x4��5x2+4��0��һ��һԪ�Ĵη��̣�
(̽��)���ݸ÷��̵��ص㣬ͨ���á���Ԫ�����ⷽ�̣�
��x2��y����ôx4��y2������ԭ���̿ɱ�Ϊ�� ����
��ã�y1��1��y2���� ����
��y��1ʱ��x2��1����x����1��
��y���� ��ʱ��x2���� ������x���� ����
ԭ������4�������ֱ����� ����
(Ӧ��)��������Ľ�����̣���ⷽ�̣�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڲ���ڼ䣬ij���̶����˼��ֲ�Ҷ90�֣����ֲ�Ҷ80�֣�����A��B�����ͺŵĻ�����20��������أ���֪A�ͻ���ÿ���˷�Ϊ0.4��Ԫ��B�ͻ���ÿ���˷�Ϊ0.6��Ԫ����13�֣�
��1����A�ͻ�������x�������˷�Ϊy��Ԫ��д��y��x�ĺ�����ϵʽ��
��2����һ��A�ͻ�����װ���ֲ�Ҷ6�֣����ֲ�Ҷ2�֣�һ��B�ͻ�����װ���ֲ�Ҷ3�֣����ֲ�Ҷ7�֣�����Ҫ����A��B�����ͺŻ���һ��������������Ҷ�������ļ������䷽����
��3��˵�����ַ����˷����٣������˷��Ƕ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
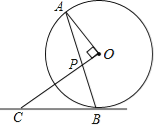
����Ŀ����ͼ��AB����O���ң�OP��OA��AB�ڵ�P������B��ֱ�߽�OP���ӳ����ڵ�C����CP=CB��
��1����֤��BC����O�����ߣ�
��2������O�İ뾶Ϊ![]() ��OP=1����BC�ij���
��OP=1����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
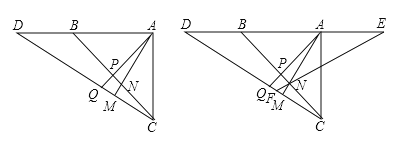
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬����
�ӳ�����һ�㣬����![]() ����
����![]() �ֱ���
�ֱ���![]() ������Ϊ
������Ϊ![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
��1����֤��![]() ��
��
��2����ͼ����![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ������
������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ����֤��
����֤��![]() ��
��
��3���ڣ�2���������£���![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() ��ֵΪ____________________��
��ֵΪ____________________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com