
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 延长线上一点,连接
延长线上一点,连接![]() ,过
,过![]() 分别作
分别作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,作
,作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,当![]() 时,请直接写出
时,请直接写出![]() 的值为____________________.
的值为____________________.
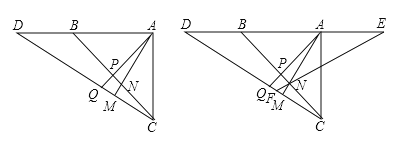
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)利用AAS证明△APN≌△CPQ,可得AN=CQ;
(2)如图2,连接BQ,证明△DBQ≌△EAN(SAS),可得DQ=EN;
(3)设AE=2x,AB=3x,则BD=2x,DC![]() x,作辅助线,构建直角三角形和相似三角形,证明△AHE∽△AMD和△DQA∽△ANC,得
x,作辅助线,构建直角三角形和相似三角形,证明△AHE∽△AMD和△DQA∽△ANC,得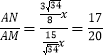 ,设AH=8m,AM=20m,AN=17m,再证明△EHN∽△FMN,即可得出结论.
,设AH=8m,AM=20m,AN=17m,再证明△EHN∽△FMN,即可得出结论.
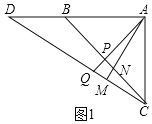
(1)如图1.
∵AP⊥BC,AM⊥CD,∴∠APN=∠CPQ=90°,∴∠PNA+∠NAP=∠NAP+∠CQP=90°,∴∠PNA=∠CQP.
∵AB=AC,∠BAC=90°,∴AP=PC,∴△APN≌△CPQ(AAS),∴AN=CQ;
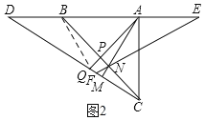
(2)如图2,连接BQ,由(1)知:AP是BC的垂直平分线,∴BQ=CQ.
∵AN=CQ,∴AN=BQ.
∵BQ=QC,∴∠QBC=∠QCB=∠NAP.
∵∠PBA=∠PAB=45°,∴∠QBA=∠BAN,∴∠DBQ=∠NAE.
∵BD=AE,∴△DBQ≌△EAN(SAS),∴DQ=EN;
(3)∵AE![]() AB,即
AB,即![]() ,∴设AE=2x,则AB=3x,BD=2x,DC
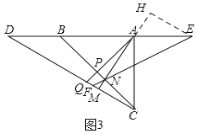
,∴设AE=2x,则AB=3x,BD=2x,DC![]() x,如图3,过E作EH⊥AM,交MA的延长线于H,∴∠H=∠AMD=90°,∴EH∥DC,∴∠HEA=∠CDA,∴△AHE∽△AMD,∴
x,如图3,过E作EH⊥AM,交MA的延长线于H,∴∠H=∠AMD=90°,∴EH∥DC,∴∠HEA=∠CDA,∴△AHE∽△AMD,∴![]() .
.
∵∠MAC=∠CDA,∠ACN=∠DAQ=45°,∴△DQA∽△ANC,∴![]() ,由(2)知:CQ=AN,∴
,由(2)知:CQ=AN,∴![]() ,∴AN=CQ
,∴AN=CQ![]() x,S△ADC
x,S△ADC![]() ,AM
,AM![]() ,∴
,∴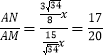 ,∴设AH=8m,AM=20m,AN=17m,则MN=3m.
,∴设AH=8m,AM=20m,AN=17m,则MN=3m.
∵EH∥FM,∴△EHN∽△FMN,∴![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
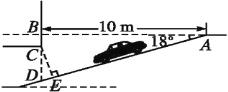
【题目】.某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出正确的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
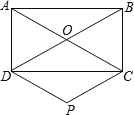
【题目】已知,如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P.
①求证:四边形CODP是菱形.
②若AD=6,AC=10,求四边形CODP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
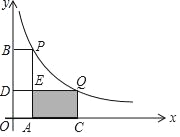
【题目】如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=![]() (k>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D,QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(k>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D,QD交PA于点E,随着m的增大,四边形ACQE的面积( )
A. 增大 B. 减小
C. 先减小后增大 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b-![]() <0的解集(直接写出答案).
<0的解集(直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
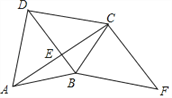
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
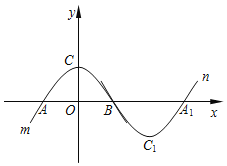
【题目】如图所示,抛物线m:![]() 与x轴于点A、
与x轴于点A、![]() 点A在点B的左侧
点A在点B的左侧![]() ,与y轴交于点
,与y轴交于点![]() 将抛物线m绕点B旋转
将抛物线m绕点B旋转![]() ,得到新的抛物线n,它的顶点为
,得到新的抛物线n,它的顶点为![]() ,与x轴的另一个交点为
,与x轴的另一个交点为![]() .
.
![]() 当
当![]() ,
,![]() 时,求抛物线n的解析式;
时,求抛物线n的解析式;
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 当
当![]() 时,四边形
时,四边形![]() 可能是矩形吗?若能,请求出抛物线m的解析式;若不能,请说明理由.
可能是矩形吗?若能,请求出抛物线m的解析式;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com