
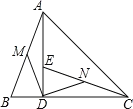
【题目】如图,在![]() 中,
中,![]() ,垂足为
,垂足为![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 分别是
分别是![]() 的中点,求
的中点,求![]() 的度数.
的度数.

【答案】90°
【解析】
由垂直的定义得到∠ADB=∠ADC=90°,根据SAS可得△ABD≌△CDE;根据全等三角形的性质得到∠BAD=∠DCE,根据直角三角形的性质得到AM=CN,由△ADM≌△CDN,可得∠ADM=∠CDN,再根据∠CDN+∠ADN=90°,可得∠ADM+∠ADN=90°,即可得出∠MDN=90°.
∵AD⊥BC,∴∠ADB=∠ADC=90°.在△ABD与△CDE中,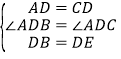 ,∴△ABD≌△CDE(SAS),∴∠BAD=∠DCE,AB=CE.
,∴△ABD≌△CDE(SAS),∴∠BAD=∠DCE,AB=CE.
∵M、N分别是AB、CE的中点,∴AM![]() AB,CN
AB,CN![]() CE,∴AM=CN.在△ADM和△CDN中,
CE,∴AM=CN.在△ADM和△CDN中,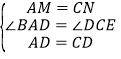 ,∴△ADM≌△CDN(SAS),∴∠ADM=∠CDN.
,∴△ADM≌△CDN(SAS),∴∠ADM=∠CDN.
∵∠CDN+∠ADN=90°,∴∠ADM+∠ADN=90°,∴∠MDN=90°.


科目:初中数学 来源: 题型:
【题目】下列命题正确的个数是
①若代数式![]() 有意义,则x的取值范围为x≤1且x≠0.
有意义,则x的取值范围为x≤1且x≠0.
②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元.
③若反比例函数![]() (m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
(m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
④若函数的图象关于y轴对称,则函数称为偶函数,下列三个函数:y=3,y=2x+1,y=x2中偶函数的个数为2个.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
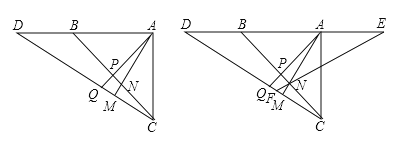
【题目】如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N.设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( )

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
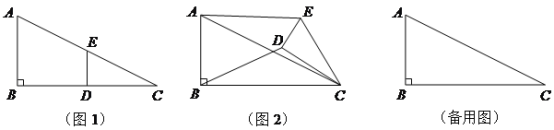
【题目】(10分)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当![]() 时,
时,![]() ;② 当
;② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 延长线上一点,连接
延长线上一点,连接![]() ,过
,过![]() 分别作
分别作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,作
,作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,当![]() 时,请直接写出
时,请直接写出![]() 的值为____________________.
的值为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3为边长作等边△A3A2B3,…,则等边△A2017A2018B2018的边长是_____.
与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3为边长作等边△A3A2B3,…,则等边△A2017A2018B2018的边长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
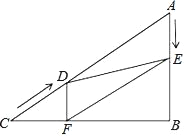
【题目】如图,在Rt△ABC中,∠B=90°,AC=40cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤10),过点D作DF⊥BC于点F,连接DE,EF.
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(2)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com