
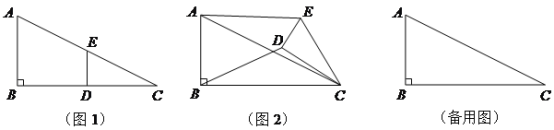
【题目】(10分)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当![]() 时,
时,![]() ;② 当
;② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
【答案】(1)①![]() ,②
,②![]() .(2)无变化;理由参见解析.(3)
.(2)无变化;理由参见解析.(3)![]() ,
,![]() .
.
【解析】
试题(1)①当α=0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出![]() 的值是多少.
的值是多少.
②α=180°时,可得AB∥DE,然后根据![]() ,求出
,求出![]() 的值是多少即可.
的值是多少即可.
(2)首先判断出∠ECA=∠DCB,再根据![]() ,判断出△ECA∽△DCB,即可求出
,判断出△ECA∽△DCB,即可求出![]() 的值是多少,进而判断出
的值是多少,进而判断出![]() 的大小没有变化即可.
的大小没有变化即可.
(3)根据题意,分两种情况:①点A,D,E所在的直线和BC平行时;②点A,D,E所在的直线和BC相交时;然后分类讨论,求出线段BD的长各是多少即可.
试题解析:(1)①当α=0°时,
∵Rt△ABC中,∠B=90°,
∴AC=![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴![]() ,BD=8÷2=4,
,BD=8÷2=4,
∴![]() .
.
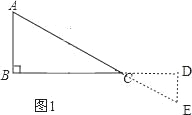
②如图1,
 ,
,
当α=180°时,
可得AB∥DE,
∵![]() ,
,
∴![]()
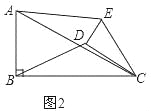
(2)如图2,
 ,
,
当0°≤α<360°时,![]() 的大小没有变化,
的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵![]() ,
,
∴△ECA∽△DCB,
∴![]() .
.
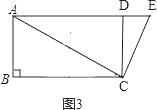
(3)①如图3,
 ,
,
∵AC=4![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD=![]()
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC=![]() .
.
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
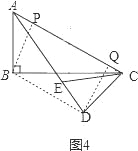 ,
,
∵AC=![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD=![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴DE=![]() =2,
=2,
∴AE=AD-DE=8-2=6,
由(2),可得
![]() ,
,
∴BD=![]() .
.
综上所述,BD的长为![]() 或
或![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
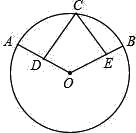
(2)如图:![]() =
=![]() ,D、E分别是半径OA和OB的中点.求证:CD=CE.
,D、E分别是半径OA和OB的中点.求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
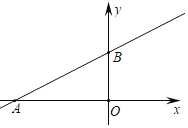
【题目】如图,直线y=![]() x+4与x轴相交于点A,与y轴相交于点B.
x+4与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BC与x轴相交于点C,若△ABC的面积是16,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形 ABCD 中,对角线 AC、BD 相交于 O,如果菱形 ABCD 的周长为 20,BD=6,则下列结论中, 正确的是( )
A.AC=8B.AC=4
C.菱形 ABCD 的面积为 48D.菱形ABCD 的高为 9.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=kx+4(k关0)与x轴,y轴分别相交于点A,B,与直线l2:y=mx(m≠0)相交于点C(1,2).
(1)求k,m的值;
(2)求点A和点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价y(单位:元/件)与时间x(单位:天)的函数关系式为y=![]() ;在第x天的销售量p(单位:件)与时间x(单位:天)的函数关系的相关信息如下表.已知商品的进价为30元/件,每天的销售利润为w(单位:元).
;在第x天的销售量p(单位:件)与时间x(单位:天)的函数关系的相关信息如下表.已知商品的进价为30元/件,每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
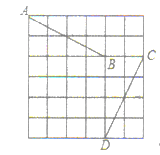
【题目】如图,![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,小明发现:线段
,小明发现:线段![]() 与线段
与线段![]() 存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.
存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com