
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌACЃН40cmЃЌЁЯAЃН60ЁуЃЌЕуDДгЕуCГіЗЂбиCAЗНЯђвд4cm/УыЕФЫйЖШЯђЕуAдШЫйдЫЖЏЃЌЭЌЪБЕуEДгЕуAГіЗЂбиABЗНЯђвд2cm/УыЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЌЕБЦфжавЛИіЕуЕНДяжеЕуЪБЃЌСэвЛИіЕувВЫцжЎЭЃжЙдЫЖЏЃЎЩшЕуDЁЂEдЫЖЏЕФЪБМфЪЧtУыЃЈ0ЃМtЁм10ЃЉЃЌЙ§ЕуDзїDFЁЭBCгкЕуFЃЌСЌНгDEЃЌEFЃЎ
ЃЈ1ЃЉЫФБпаЮAEFDФмЙЛГЩЮЊСтаЮТ№ЃПШчЙћФмЃЌЧѓГіЯргІЕФtжЕЃЛШчЙћВЛФмЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃПЧыЫЕУїРэгЩЃЎ
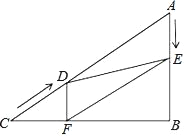
ЁОД№АИЁПЃЈ1ЃЉФмЃЌЕБtЃН![]() УыЪБЃЌЫФБпаЮAEFDЮЊСтаЮЃЌМћНтЮіЃЛЃЈ2ЃЉЕБtЃН8Лђ5УыЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃЌМћНтЮі.
УыЪБЃЌЫФБпаЮAEFDЮЊСтаЮЃЌМћНтЮіЃЛЃЈ2ЃЉЕБtЃН8Лђ5УыЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃЌМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉФмЃЎЪзЯШжЄУїЫФБпаЮAEFDЮЊЦНааЫФБпаЮЃЌЕБAEЃНADЪБЃЌЫФБпаЮAEFDЮЊСтаЮЃЌМД40Љ4tЃН2tЃЌНтЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЗжШ§жжЧщаЮЬжТлМДПЩЃЎ
ЃЈ1ЃЉжЄУїЃКФмЃЎ
РэгЩШчЯТЃКдкЁїDFCжаЃЌЁЯDFCЃН90ЁуЃЌЁЯCЃН30ЁуЃЌDCЃН4tЃЌ
ЁрDFЃН2tЃЌ
гжЁпAEЃН2tЃЌ
ЁрAEЃНDFЃЌ
ЁпABЁЭBCЃЌDFЁЭBCЃЌ
ЁрAEЁЮDFЃЌ
гжЁпAEЃНDFЃЌ
ЁрЫФБпаЮAEFDЮЊЦНааЫФБпаЮЃЌ
ЕБAEЃНADЪБЃЌЫФБпаЮAEFDЮЊСтаЮЃЌ
МД40Љ4tЃН2tЃЌНтЕУtЃН![]() ЃЎ
ЃЎ
ЁрЕБtЃН![]() УыЪБЃЌЫФБпаЮAEFDЮЊСтаЮЃЎ
УыЪБЃЌЫФБпаЮAEFDЮЊСтаЮЃЎ
ЃЈ2ЃЉЂйЕБЁЯDEFЃН90ЁуЪБЃЌгЩЃЈ1ЃЉжЊЫФБпаЮAEFDЮЊЦНааЫФБпаЮЃЌ
ЁрEFЁЮADЃЌ
ЁрЁЯADEЃНЁЯDEFЃН90ЁуЃЌ
ЁпЁЯAЃН60ЁуЃЌ
ЁрЁЯAEDЃН30ЁуЃЌ
ЁрADЃН![]() AEЃНtЃЌ
AEЃНtЃЌ
гжADЃН40Љ4tЃЌМД40Љ4tЃНtЃЌНтЕУtЃН8ЃЛ
ЂкЕБЁЯEDFЃН90ЁуЪБЃЌЫФБпаЮEBFDЮЊОиаЮЃЌдкRtЁїAEDжаЁЯAЃН60ЁуЃЌдђЁЯADEЃН30ЁуЃЌ
ЁрADЃН2AEЃЌМД40Љ4tЃН4tЃЌНтЕУtЃН5ЃЎ
ЂлШєЁЯEFDЃН90ЁуЃЌдђEгыBжиКЯЃЌDгыAжиКЯЃЌДЫжжЧщПіВЛДцдкЃЎ
злЩЯЫљЪіЃЌЕБtЃН8Лђ5УыЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФжаЕуЃЌЧѓ
ЕФжаЕуЃЌЧѓ![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌШєx1x2+y1y2ЃН0ЃЌЧвAЃЌBОљВЛЮЊдЕуЃЌдђГЦAКЭBЛЅЮЊе§НЛЕуЃЎБШШчЃКAЃЈ1ЃЌ1ЃЉЃЌBЃЈ2ЃЌЉ2ЃЉЃЌЦфжа1ЁС2+1ЁСЃЈЉ2ЃЉЃН0ЃЌФЧУДAКЭBЛЅЮЊе§НЛЕуЃЎ
ЃЈ1ЃЉЕуPКЭQЛЅЮЊе§НЛЕуЃЌPЕФзјБъЮЊЃЈЉ2ЃЌ3ЃЉЃЌ
ЂйШчЙћQЕФзјБъЮЊЃЈ6ЃЌmЃЉЃЌФЧУДmЕФжЕЮЊЖрЩйЃЛ
ЂкШчЙћQЕФзјБъЮЊЃЈxЃЌyЃЉЃЌЧѓyгыxжЎМфЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕуMКЭNЛЅЮЊе§НЛЕуЃЌжБНгаДГіЁЯMONЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЕуCЃЌDЪЧвдЃЈ0ЃЌ2ЃЉЮЊдВаФЃЌАыОЖЮЊ2ЕФдВЩЯЕФе§НЛЕуЃЌвдЯпЖЮCDЮЊБпЃЌЙЙдье§ЗНаЮCDEFЃЌдВаФFдке§ЗНаЮCDEFЕФЭтВПЃЌЧѓЯпЖЮOEГЄЖШЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
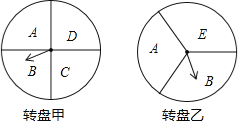
ЁОЬтФПЁПФГГЌЪадкЖЫЮчНкЦкМфПЊеЙгХЛнЛюЖЏЃЌЗВЙКЮяепПЩвдЭЈЙ§зЊЖЏзЊХЬЕФЗНЪНЯэЪмелПлгХЛнЃЌБОДЮЛюЖЏЙВгаСНжжЗНЪНЃЌЗНЪНвЛЃКзЊЖЏзЊХЬМзЃЌжИеыжИЯђAЧјгђЪБЃЌЫљЙКТђЮяЦЗЯэЪм9елгХЛнЁЂжИеыжИЯђЦфЫќЧјгђЮогХЛнЃЛЗНЪНЖўЃКЭЌЪБзЊЖЏзЊХЬМзКЭзЊХЬввЃЌШєСНИізЊХЬЕФжИеыжИЯђУПИіЧјгђЕФзжФИЯрЭЌЃЌЫљЙКТђЮяЦЗЯэЪм8елгХЛнЃЌЦфЫќЧщПіЮогХЛнЃЎдкУПИізЊХЬжаЃЌжИеыжИЯђУПИіЧјГЧЕФПЩФмадЯрЭЌЃЈШєжИеыжИЯђЗжНчЯпЃЌдђжиаТзЊЖЏзЊХЬЃЉ
ЃЈ1ЃЉШєЙЫПЭбЁдёЗНЪНвЛЃЌдђЯэЪм9елгХЛнЕФИХТЪЮЊЖрЩйЃЛ
ЃЈ2ЃЉШєЙЫПЭбЁдёЗНЪНЖўЃЌЧыгУЪїзДЭМЛђСаБэЗЈСаГіЫљгаПЩФмЃЌВЂЧѓЙЫПЭЯэЪм8елгХЛнЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90Ёу,AB=5,AC=3,ЕуDЪЧBCЩЯвЛЖЏЕуЃЌСЌНгADЃЌНЋЁїACDбиADелЕўЃЌЕуCТфдкЕуC'ДІЃЌСЌНгC'DНЛABгкЕуEЃЌСЌНгBC'ЃЌЕБЁїBC'DЪЧжБНЧШ§НЧаЮЪБЃЌDEЕФГЄЮЊ_________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌХзЮяЯпmЃК![]() гыxжсгкЕуAЁЂ
гыxжсгкЕуAЁЂ![]() ЕуAдкЕуBЕФзѓВр
ЕуAдкЕуBЕФзѓВр![]() ЃЌгыyжсНЛгкЕу
ЃЌгыyжсНЛгкЕу![]() НЋХзЮяЯпmШЦЕуBа§зЊ
НЋХзЮяЯпmШЦЕуBа§зЊ![]() ЃЌЕУЕНаТЕФХзЮяЯпnЃЌЫќЕФЖЅЕуЮЊ
ЃЌЕУЕНаТЕФХзЮяЯпnЃЌЫќЕФЖЅЕуЮЊ![]() ЃЌгыxжсЕФСэвЛИіНЛЕуЮЊ
ЃЌгыxжсЕФСэвЛИіНЛЕуЮЊ![]() ЃЎ
ЃЎ
![]() ЕБ
ЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЧѓХзЮяЯпnЕФНтЮіЪНЃЛ
ЪБЃЌЧѓХзЮяЯпnЕФНтЮіЪНЃЛ
![]() ЧѓжЄЃКЫФБпаЮ
ЧѓжЄЃКЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
![]() ЕБ
ЕБ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ПЩФмЪЧОиаЮТ№ЃПШєФмЃЌЧыЧѓГіХзЮяЯпmЕФНтЮіЪНЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ПЩФмЪЧОиаЮТ№ЃПШєФмЃЌЧыЧѓГіХзЮяЯпmЕФНтЮіЪНЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
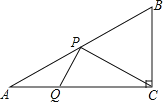
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯBAC=30ЁуЃЌаББпAB=2![]() ЃЌЖЏЕуPдкABБпЩЯЃЌЖЏЕуQдкACБпЩЯЃЌЧвЁЯCPQ=90ЁуЃЌдђЯпЖЮCQГЄЕФзюаЁжЕ=__________ .
ЃЌЖЏЕуPдкABБпЩЯЃЌЖЏЕуQдкACБпЩЯЃЌЧвЁЯCPQ=90ЁуЃЌдђЯпЖЮCQГЄЕФзюаЁжЕ=__________ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
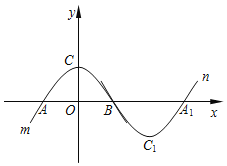
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гыжБЯп
гыжБЯп![]() НЛгкAЃЌBСНЕуЃЌНЛxжсгкDЃЌCСНЕуЃЌвбжЊ
НЛгкAЃЌBСНЕуЃЌНЛxжсгкDЃЌCСНЕуЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() ЧѓХзЮяЯпЕФКЏЪ§БэДяЪНВЂаДГіХзЮяЯпЕФЖдГЦжсЃЛ
ЧѓХзЮяЯпЕФКЏЪ§БэДяЪНВЂаДГіХзЮяЯпЕФЖдГЦжсЃЛ
![]() дкжБЯпABЯТЗНЕФХзЮяЯпЩЯЪЧЗёДцдквЛЕуEЃЌЪЙЕУ
дкжБЯпABЯТЗНЕФХзЮяЯпЩЯЪЧЗёДцдквЛЕуEЃЌЪЙЕУ![]() ЕФУцЛ§зюДѓЃПШчЙћДцдкЃЌЧѓГіEЕузјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФУцЛ§зюДѓЃПШчЙћДцдкЃЌЧѓГіEЕузјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
![]() ЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌСЌНгPAЃЌЙ§ЕуPзї
ЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌСЌНгPAЃЌЙ§ЕуPзї![]() НЛyжсгкЕуQЃЌЮЪЃКЪЧЗёДцдкЕуPЃЌЪЙЕУвдAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгы
НЛyжсгкЕуQЃЌЮЪЃКЪЧЗёДцдкЕуPЃЌЪЙЕУвдAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгы![]() ЯрЫЦЃПШєДцдкЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФPЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЯрЫЦЃПШєДцдкЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФPЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
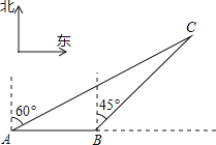
ЁОЬтФПЁПШчЭМЃК007гцДЌдкФЯКЃКЃУцЩЯбие§ЖЋЗНЯђдШЫйКНааЃЌдкAЕуЙлВтЕНгцДЌCдкББЦЋЖЋ60ЁуЗНЯђЕФЮвЙњФГДЋЭГгцГЁВЖгузївЕЃЎШє007гцДЌКНЯђВЛБфЃЌКНааАыаЁЪБКѓЕНДяBЕуЃЌЙлВтЕНгцДЌCдкЖЋББЗНЯђЩЯЃЎЮЪЃК007гцДЌдйАДдКНЯђКНааЖрГЄЪБМфЃЌРыгцДЌCЕФОрРызюНќЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com