
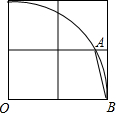
 如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为2+$\sqrt{3}$.
如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为2+$\sqrt{3}$. 分析 连接OA,过点A作AC⊥OB于点C,由题意知AC=1、OA=OB=2,从而得出OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{3}$、BC=OB-OC=2-$\sqrt{3}$,在Rt△ABC中,根据tan∠ABO=$\frac{AC}{BC}$可得答案.
解答 解:如图,连接OA,过点A作AC⊥OB于点C,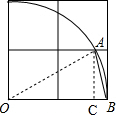
则AC=1,OA=OB=2,
∵在Rt△AOC中,OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴BC=OB-OC=2-$\sqrt{3}$,
∴在Rt△ABC中,tan∠ABO=$\frac{AC}{BC}$=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$.
故答案是:2+$\sqrt{3}$.
点评 本题主要考查解直角三角形,根据题意构建一个以∠ABO为内角的直角三角形是解题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:选择题
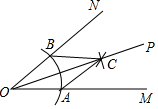 如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )
如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
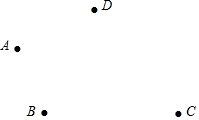 如图,平面上有四个点A,B,C,D,按照以下要求完成问题:
如图,平面上有四个点A,B,C,D,按照以下要求完成问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 测量该四边形的对角线是否互相垂直 | |
| B. | 测量该四边形的对角线是否相等 | |
| C. | 测量该四边形的对角线是否互相平分 | |
| D. | 测量该四边形的四条边是否都相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,7) | B. | (-7,3) | C. | (3,7) | D. | (7,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com