
【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.
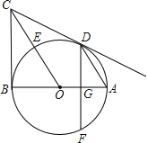
(1)求证:点E是![]() 的中点;
的中点;
(2)求证:CD是⊙O的切线;
(3)若sin∠BAD=![]() ,⊙O的半径为5,求DF的长.
,⊙O的半径为5,求DF的长.
【答案】(1)见解析 (2)见解析 (3)![]()
【解析】
(1) 连接OD,根据平行的性质得到∠A=∠COB,再证明∠DOC=∠BOC即可得到答案;
(2)先根据题意的大△COD≌△COB,再根据全等三角形的性质以及BC⊥AB于点B即可证明;
(3)先根据sin∠BAD=![]() ,设DG=4x,AD=5x再根据勾股定理求解即可得到答案;
,设DG=4x,AD=5x再根据勾股定理求解即可得到答案;
(1)证明:连接OD,
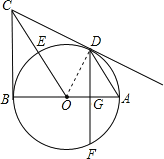
∵AD∥OC,
∴ ∠A=∠COB(两直线平行,同位角相等),
又∵∠A=![]() ∠BOD(同弧圆心角等于圆周角的2倍),
∠BOD(同弧圆心角等于圆周角的2倍),
∴∠BOC=![]() ∠BOD;
∠BOD;
∴∠DOC=∠BOC;
∴![]() ,则点E是
,则点E是![]() 的中点;
的中点;
(2)证明:如图所示:

由(1)知∠DOE=∠BOE,
∵CO=CO,OD=OB,
∴ △COD≌△COB;
∴∠CDO=∠B;
又∵BC⊥AB,
∴ ∠CDO=∠B=90°;
∴CD是⊙O的切线;
(3)解:在△ADG中,
∵sin∠BAD=![]() ,
,
设DG=4x,AD=5x;
∵ DF⊥AB,
∴ AG=3x;
又∵⊙O的半径为5,
∴ OG=5﹣3x;
∵ OD2=DG2+OG2,
∴![]() ,
,
∴ x1=![]() ,x2=0;(舍去)
,x2=0;(舍去)
∴ DF=2DG=2×4x=8x=![]() ;
;


科目:初中数学 来源: 题型:
【题目】某地为了促进旅游业的发展,要在如图所示的三条公路![]() ,
,![]() ,
,![]() 围成的一块地上修建一个度假村,要使这个度假村到
围成的一块地上修建一个度假村,要使这个度假村到![]() ,
,![]() 两条公路的距离相等,且到
两条公路的距离相等,且到![]() ,
,![]() 两地的距离相等,下列选址方法绘图描述正确的是( )
两地的距离相等,下列选址方法绘图描述正确的是( )
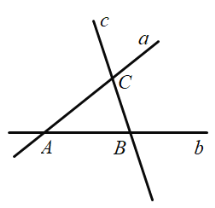
A.画![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,两线的交点符合选址条件
的垂直平分线,两线的交点符合选址条件
B.先画![]() 和
和![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,三线的交点符合选址条件
的垂直平分线,三线的交点符合选址条件
C.画三个角![]() ,
,![]() 和
和![]() 三个角的平分线,交点即为所求
三个角的平分线,交点即为所求
D.画![]() ,
,![]() ,
,![]() 三条线段的垂直平分线,交点即为所求
三条线段的垂直平分线,交点即为所求
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲,乙,丙三名校排球队员每人10次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.

(1)若运动员丙测试成绩的平均数和众数都是7,则成绩统计表中a= ,b= ;
(2)若在三名队员中选择一位垫球成绩优秀且较为稳定的同学作为排球比赛的自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() ,
,![]() ,
,![]() )
)
(3)训练期间甲、乙、丙三人之间进行随机传球游戏,先由甲传出球,经过三次传球,球回到甲手中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
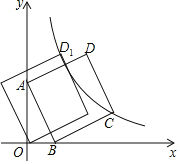
【题目】如图,直线AB与x的正半轴交于点B,且B(1,0),与y的正半轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=![]() (k≠0)上,将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线y=![]() (k≠0)上的点D1处,则k=_____.
(k≠0)上的点D1处,则k=_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
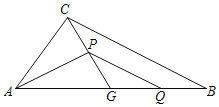
【题目】如图,在△ABC中,G为边AB中点,∠AGC=α.Q为线段BG上一动点(不与点B重合),点P在中线CG上,连接PA,PQ,记BQ=kGP.
(1)若α=60°,k=1,
①当BQ=![]() BG时,求∠PAG的度数.
BG时,求∠PAG的度数.
②写出线段PA、PQ的数量关系,并说明理由.
(2)当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
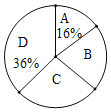
【题目】2020年4月是我国第32个爱国卫生月.某校九年级通过网课举行了主题为“防疫有我,爱卫同行”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
(1)本次调查一共随机抽取了____个参赛学生的成绩;
(2)表1中a=__;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是__;
(4)统计图中B组所占的百分比是_______;
(5)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生人数.
表1 知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A | 60≤x<70 | a |
B | 70≤x<80 | 10 |
C | 80≤x<90 | 14 |
D | 90≤x<100 | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一组数据2,2,3,4,这组数据的中位数是2
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D. 某日最高气温是![]() ,最低气温是
,最低气温是![]() ,则该日气温的极差是
,则该日气温的极差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
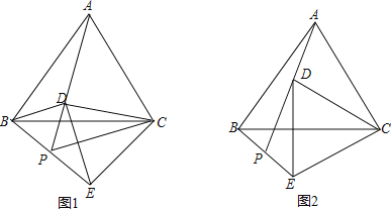
【题目】已知:△ABC是等边三角形,点D是△ABC(包含边界)平面内一点,连接CD,将线段CD绕C逆时针旋转60°得到线段CE,连接BE,DE,AD,并延长AD交BE于点P.
(1)观察填空:当点D在图1所示的位置时,填空:
①与△ACD全等的三角形是______.
②∠APB的度数为______.
(2)猜想证明:在图1中,猜想线段PD,PE,PC之间有什么数量关系?并证明你的猜想.
(3)拓展应用:如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
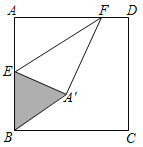
【题目】如图,四边形ABCD是边长为m的正方形,若AF=![]() m,E为AB上一点且BE=3,把△AEF沿着EF折叠,得到△A'EF,若△BA'E为直角三角形,则m的值为_____.
m,E为AB上一点且BE=3,把△AEF沿着EF折叠,得到△A'EF,若△BA'E为直角三角形,则m的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com