
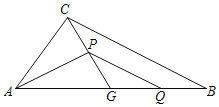
【题目】如图,在△ABC中,G为边AB中点,∠AGC=α.Q为线段BG上一动点(不与点B重合),点P在中线CG上,连接PA,PQ,记BQ=kGP.
(1)若α=60°,k=1,
①当BQ=![]() BG时,求∠PAG的度数.
BG时,求∠PAG的度数.
②写出线段PA、PQ的数量关系,并说明理由.
(2)当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
【答案】(1)①30°;②PA=PQ,见解析;(2)存在,k=![]() ,理由见解析
,理由见解析
【解析】
(1)①在GC上取点M,使得GM=GA,连接AM,再说明△AGM是等边三角形,进而得到AG=BG=2BQ,从而判定GP=MP,即AP平分∠MAG即可解答;②先说明△PGN是等边三角形,进而得到GQ=AN,从而证明△ANB≌△QGP即可解答;
(2)先说明PH=PG,∠PHA=∠PGQ=135°,得出HG=BQ,再判断出AH=GQ,进而得出△AHP≌△QGP即可.
解:(1)①如图1,在GC上取点M,使得GM=GA,连接AM,
∵∠AGM=α=60°,
∴△AGM为等边三角形,
∴AG=GM,∠MAG=60°,
∵G为AB的中点,Q为GB的中点,
∴AG=BG=2BQ,
∵k=1,
∴BQ=GP,
∴GM=AG=BG=MG=2GP,
∴GP=MP,
∴AP平分∠MAG,
∴∠PAG=∠PAM=30°;
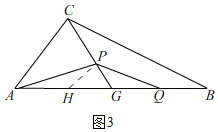
②如图2,在AG上取点N,连接PN,使得PN=PG,
∵∠PGN=60°,
∴△PGN是等边三角形,
∵BG=GA,
∴BQ=PG=PN=NG=GQ,
∴GQ=AN,
∵∠ANP=∠QGP,
∴△ANB≌△QGP(SAS),
∴PA=PQ;
(2)存在,k=![]() ,使得②中的结论成立;
,使得②中的结论成立;
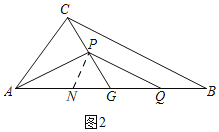
证明:如图3,过点P作PG的垂线交AG于点H.
∵∠AGC=45°,
∴∠PHG=45°,
∴PH=PG,∠PHA=∠PGQ=135°,
∵![]() ,
,![]() ,
,
∴HG=BQ,
∵AG=BG,
∴AH=GQ.
∴△AHP≌△QGP(SAS)
∴PA=PQ.



 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】某单位在疫情期间用3000元购进A、B两种口罩1100个,购买A种口罩与购买B种口罩的费用相同,且A种口罩的单价是B种口罩单价的1.2倍;
(1)求A,B两种口罩的单价各是多少元?
(2)若计划用不超过7000元的资金再次购进A、B两种口罩共2600个,已知A、B两种口罩的进价不变,求A种口罩最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某学校高中两个班的学生上学时步行、骑车、乘公交、乘私家车人数的扇形统计图,已知乘公交人数是乘私家车人数的2倍.若步行人数是18人,则下列结论正确的是( )

A. 被调查的学生人数为90人
B. 乘私家车的学生人数为9人
C. 乘公交车的学生人数为20人
D. 骑车的学生人数为16人
查看答案和解析>>
科目:初中数学 来源: 题型:
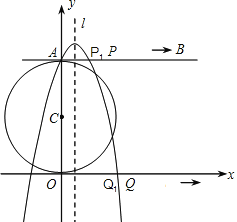
【题目】如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线.动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q从点A和点O同时出发,设运动时间为t(秒).
(1)当t=1时,得到P1、Q1,求经过A、P1、Q1三点的抛物线解析式及对称轴l;
(2)当t为何值时,直线PQ与⊙C相切?并写出此时点P和点Q的坐标;
(3)在(2)的条件下,抛物线对称轴l上存在一点N,使NP+NQ最小,求出点N的坐标并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
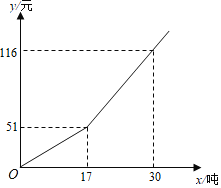
【题目】某市为了倡导居民节约用水,生活用自来水按阶梯式水价计费.如图是居民每户每月的水(自来水)费y(元)与所用的水(自来水)量x(吨)之间的函数图象.根据如图图象提供的信息,解答下列问题:
(1)当一户居民在某月用水为15吨时,求这户居民这个月的水费.
(2)当17≤x≤30时,求y与x之间的函数关系式;并计算某户居民上月水费为91元时,这户居民上月用水量多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.
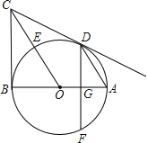
(1)求证:点E是![]() 的中点;
的中点;
(2)求证:CD是⊙O的切线;
(3)若sin∠BAD=![]() ,⊙O的半径为5,求DF的长.
,⊙O的半径为5,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处40![]() 米的点D(点D与楼底C在同一水平面上)出发,沿与地面成30°角的斜面DB前进20米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
米的点D(点D与楼底C在同一水平面上)出发,沿与地面成30°角的斜面DB前进20米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com