
【题目】某市为了倡导居民节约用水,生活用自来水按阶梯式水价计费.如图是居民每户每月的水(自来水)费y(元)与所用的水(自来水)量x(吨)之间的函数图象.根据如图图象提供的信息,解答下列问题:
(1)当一户居民在某月用水为15吨时,求这户居民这个月的水费.
(2)当17≤x≤30时,求y与x之间的函数关系式;并计算某户居民上月水费为91元时,这户居民上月用水量多少吨?
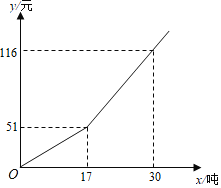
【答案】(1)当一户居民在某月用水为15吨时,这户居民这个月的水费是45元;(2)当17≤x≤30时,y与x之间的函数关系式是y=5x﹣34,某户居民上月水费为91元时,这户居民上月用水量为25吨
【解析】
(1)当用水为15吨时,通过观察图象得出每吨水的价格为51÷17=3(元),进而求解即可;
(2)当17≤x≤30时,y与x之间图象是一条直线的一部分,因此设函数解系式为y=kx+b,用待定系数法求出解析式,令y=91,求x的值即可.
解:(1)由图象可得,
当0≤x≤17时,每吨水的价格为51÷17=3(元),
15×3=45(元),
答:当一户居民在某月用水为15吨时,这户居民这个月的水费是45元;
(2)当17≤x≤30时,设y与x之间的函数关系式是y=kx+b,
![]() ,得
,得![]() ,
,
即当17≤x≤30时,y与x之间的函数关系式是y=5x﹣34,
当y=91时,91=5x﹣34,得x=25,
答:当17≤x≤30时,y与x之间的函数关系式是y=5x﹣34,某户居民上月水费为91元时,这户居民上月用水量为25吨.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:
速度v(千米/小时) | …… | 5 | 10 | 20 | 32 | 40 | 48 | …… |
流量q(辆/小时) | …… | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | …… |
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是___________.(只填上正确答案的序号)
①q=90v+100;②q=![]() ;③q=2v2+120v.
;③q=2v2+120v.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当18≤v≤28该路段不会出现交通拥堵现象.试分析当车流密度k在什么范围时,该路段不会出现交通拥堵现象;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,当d=25米时请求出此时的速度v.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC
(Ⅰ)求证:AC是⊙O的切线;
(Ⅱ)若BF=5,DF=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
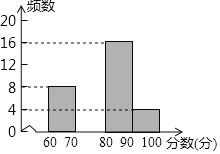
请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学. 学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC与BD交于点O,AD=1,DC=![]() ,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
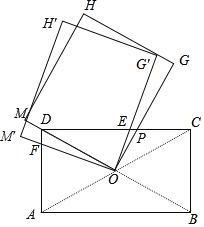
A.y=![]() xB.y=
xB.y=![]() xC.y=
xC.y=![]() xD.y=
xD.y=![]() x
x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,G为边AB中点,∠AGC=α.Q为线段BG上一动点(不与点B重合),点P在中线CG上,连接PA,PQ,记BQ=kGP.
(1)若α=60°,k=1,
①当BQ=![]() BG时,求∠PAG的度数.
BG时,求∠PAG的度数.
②写出线段PA、PQ的数量关系,并说明理由.
(2)当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
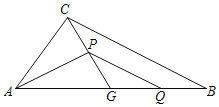
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,OM是∠AOB的平分线,将一个直角三角板的直角顶点P放在射线OM上,OP=2,移动直角三角板,两边分别交射线OA,OB与点C,D.
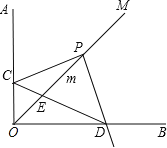
(1)如图,当点C、D都不与点O重合时,求证:PC=PD;
(2)联结CD,交OM于E,设CD=x,PE=y,求y与x之间的函数关系式;
(3)如图,若三角板的一条直角边与射线OB交于点D,另一直角边与直线OA,直线OB分别交于点C,F,且△PDF与△OCD相似,求OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线经过点D(﹣2,﹣3)和点E(3,2),点P是第一象限抛物线上的一个动点.
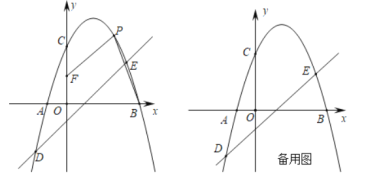
(1)求直线DE和抛物线的表达式;
(2)在y轴上取点F(0,1),连接PF,PB,当四边形OBPF的面积是7时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴的右侧时,直线DE上存在两点M,N(点M在点N的上方),且MN=2![]() ,动点Q从点P出发,沿P→M→N→A的路线运动到终点A,当点Q的运动路程最短时,请直接写出此时点N的坐标.
,动点Q从点P出发,沿P→M→N→A的路线运动到终点A,当点Q的运动路程最短时,请直接写出此时点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com