
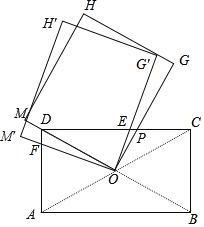
【题目】如图,矩形ABCD的对角线AC与BD交于点O,AD=1,DC=![]() ,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
A.y=![]() xB.y=
xB.y=![]() xC.y=
xC.y=![]() xD.y=
xD.y=![]() x
x
【答案】A
【解析】
根据矩形的性质和余角的性质可得∠OPD=∠ODF,进而可证明△DFO∽△PEO,于是有![]() ,由矩形的性质和等腰三角形的性质可得∠ODC=∠OCD,然后根据其正切相等即可得到
,由矩形的性质和等腰三角形的性质可得∠ODC=∠OCD,然后根据其正切相等即可得到![]() 的值,进一步即可求出答案.
的值,进一步即可求出答案.
解:∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO,∠ADC=90°,
∴DO=CO,
∴∠ODC=∠OCD,
∵四边形OGHM是矩形,
∴∠MOG=90°,
∴∠ODC+∠OPD=90°,
又∵∠ODC+∠ODF=90°,
∴∠OPD=∠ODF,
∵将矩形OGHM绕点O逆时针方向旋转α,
∴∠DOF=∠POE,
∴△DFO∽△PEO,
∴![]() ,
,
∵∠ODC=∠OCD,
∴tan∠OCD=tan∠ODC,
∴![]() ,
,
∵AD=1,DC=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故选:A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
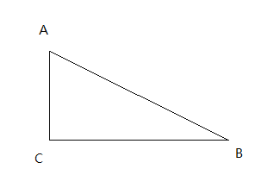
【题目】如图,在Rt△ABC中,∠ACB=90°
(1)请用尺规作图法,作∠ACB的平分线CD,交AB于点D;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,过点D分别作DE![]() AC于点E,DF
AC于点E,DF![]() BC于点F,四边形CEDF_____形
BC于点F,四边形CEDF_____形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:①b2﹣4ac=0 ②a+b+c>0 ③2a﹣b=0④c﹣a=3,其中正确的有_____.(填序号)
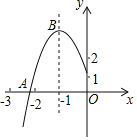
查看答案和解析>>
科目:初中数学 来源: 题型:
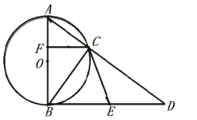
【题目】如图,⊙O是![]() ABC的外接圆,AB是圆的直径,直线AC与过B点的切线相交于点D,E是BD的中点,连接CE.
ABC的外接圆,AB是圆的直径,直线AC与过B点的切线相交于点D,E是BD的中点,连接CE.
(1)求证:CE是圆O的切线;
(2)如图,CF⊥AB,垂足为F,若⊙O的半径为3,BE=4,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,![]() ).
).
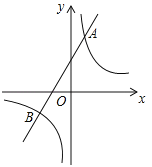
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
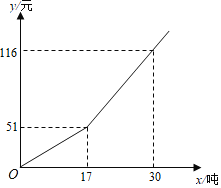
【题目】某市为了倡导居民节约用水,生活用自来水按阶梯式水价计费.如图是居民每户每月的水(自来水)费y(元)与所用的水(自来水)量x(吨)之间的函数图象.根据如图图象提供的信息,解答下列问题:
(1)当一户居民在某月用水为15吨时,求这户居民这个月的水费.
(2)当17≤x≤30时,求y与x之间的函数关系式;并计算某户居民上月水费为91元时,这户居民上月用水量多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲转盘被分成3个面积相等的扇形,乙转盘被分成2个半圆,每一个扇形或半圆都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转一次,直到指针指向一个区域为止).
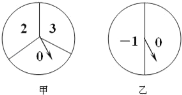
(1)请你用画树状图或列表格的方法,列出所有等可能情况,并求出点(x,y)落在坐标轴上的概率;
(2)直接写出点(x,y)落在以坐标原点为圆心,2为半径的圆内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com