
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,![]() ).
).
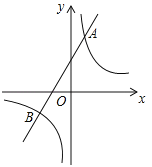
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)把A的坐标代入反比例函数的解析式,求出m的值,从而确定反比例函数的解析式,把B的坐标代入反比例函数解析式求出B的坐标,把A、B的坐标代入一次函数的解析式,即可求出a,b的值,从而确定一次函数的解析式;
(2)根据函数的图象即可得出一次函数的值小于反比例函数的值的x的取值范围.
解:(1)∵反比例函数y=![]() 的图象过点A(1,4),
的图象过点A(1,4),
∴4=![]() ,即m=4,
,即m=4,
∴反比例函数的解析式为:y=![]() .
.
∵反比例函数y=![]() 的图象过点B(n,﹣2),
的图象过点B(n,﹣2),
∴﹣2=![]() ,
,
解得:n=﹣2
∴B(﹣2,﹣2).
∵一次函数y=ax+b(k≠0)的图象过点A(1,4)和点B(﹣2,﹣2),
∴![]() ,
,
解得![]() .
.
∴一次函数的解析式为:y=2x+2;
(2)由图象可知:当x<﹣2或0<x<1时,一次函数的值小于反比例函数的值.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A和∠B的平分线交于点P,过点P作PE⊥AB交AB于点E.若BC=5,AC=12,则AE等于______ .
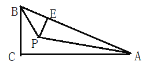
查看答案和解析>>
科目:初中数学 来源: 题型:
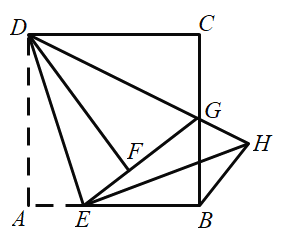
【题目】如图,在正方形ABCD中,E为边AB上一点,沿DE将![]() 折叠得到
折叠得到![]() ,延长EF交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
,延长EF交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)探求BH与AE数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
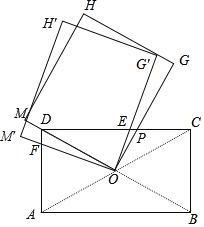
【题目】如图,矩形ABCD的对角线AC与BD交于点O,AD=1,DC=![]() ,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
A.y=![]() xB.y=
xB.y=![]() xC.y=
xC.y=![]() xD.y=
xD.y=![]() x
x
查看答案和解析>>
科目:初中数学 来源: 题型:
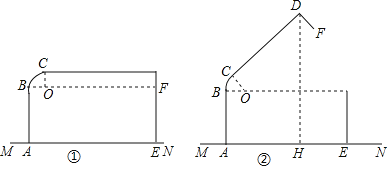
【题目】如图①是一个小箱子ABCDE放在桌面MN上的示意图,BC这部分可弯曲,在弯曲时形成一段圆弧,设圆弧所在圆的圆心为O,线段AB,CD均与圆弧相切,点B,C分别为切点,小箱子盖面CD与桌面MN平行,此时CD距离桌面14cm,已知AB的长10cm,CD的长为25.2cm.
(1)如图①,求弧BC的长度(结果保留π).
(2)如图②,若小箱子ABCDE打开后弧BC所对的圆心角度数为60°,求小箱子顶端D到桌面MN的距离DH(结果保留一位小数).(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市平时每天都将一定数量的白糖和红糖进行包装以便出售,已知每天包装白糖的质量是包装红糖质量的![]() 倍,且每天包装白糖和红糖的质量之和为45千克.
倍,且每天包装白糖和红糖的质量之和为45千克.
(1)求平均每天包装白糖和红糖的质量各是多少千克?
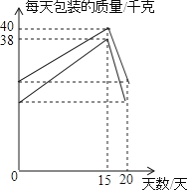
(2)为迎接今年6月25日的“端午节”,该超市决定在前20天增加每天包装白糖和红糖的质量,二者的包装质量与天数的变化情况如图所示,节日后又恢复到原来每天的包装质量.直接写出在这20天内每天包装白糖和红糖的质量随天数变化的函数关系式,并写出自变量的取值范围.
(3)假设该超市每天都会将当天包装后的白糖和红糖全部售出,已知白糖的成本价为每千克3.9元,红糖的成本每千克5.5元,二者包装费用平均每千克均为0.5元,白糖售价为每千克6元,红糖售价为每千克8元,那么在这20天中有哪几天销售白糖和红糖的利润之和大于120元?[总利润=售价额﹣成本﹣包装费用].
查看答案和解析>>
科目:初中数学 来源: 题型:
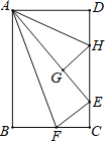
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com