
【题目】某超市平时每天都将一定数量的白糖和红糖进行包装以便出售,已知每天包装白糖的质量是包装红糖质量的![]() 倍,且每天包装白糖和红糖的质量之和为45千克.
倍,且每天包装白糖和红糖的质量之和为45千克.
(1)求平均每天包装白糖和红糖的质量各是多少千克?
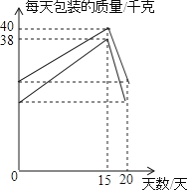
(2)为迎接今年6月25日的“端午节”,该超市决定在前20天增加每天包装白糖和红糖的质量,二者的包装质量与天数的变化情况如图所示,节日后又恢复到原来每天的包装质量.直接写出在这20天内每天包装白糖和红糖的质量随天数变化的函数关系式,并写出自变量的取值范围.
(3)假设该超市每天都会将当天包装后的白糖和红糖全部售出,已知白糖的成本价为每千克3.9元,红糖的成本每千克5.5元,二者包装费用平均每千克均为0.5元,白糖售价为每千克6元,红糖售价为每千克8元,那么在这20天中有哪几天销售白糖和红糖的利润之和大于120元?[总利润=售价额﹣成本﹣包装费用].
【答案】(1)平均每天包装白糖和红糖的质量分别为25千克和20千克;(2) ;(3)第11,12,13,14,15,16天中销售白糖和红糖的总利润大于120元
;(3)第11,12,13,14,15,16天中销售白糖和红糖的总利润大于120元
【解析】
(1)分别设白糖和红糖的质量,根据题意列方程组解出即可;
(2)分0≤x≤15和15<x≤20两种情况讨论:根据图中的信息利用待定系数法求直线的解析式,即可得到这20天内每天包装白糖和红糖的质量随天数变化的函数关系式;
(3)设销售白糖和红糖的利润之和为W元,设分0≤x≤15和15<x≤20两种情况讨论:由题意得出W与x的有关系式,列不等式解出求x的取值范围,并取整数解.
解:(1)设平均每天包装白糖和红糖的质量分别为a千克和b千克,
则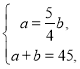 解得
解得![]() .
.
答:平均每天包装白糖和红糖的质量分别为25千克和20千克.
(2))设每天包装白糖的质量与天数的关系式为:y1=kx+b1,每天包装红糖的质量与天数的关系式为:y2=ax+b2,
①当0≤x≤15时,由图象知:y1=kx+b1过(15,40)、(0,25),
列方程组得
解得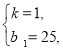
∴y1=x+25,
由图象知:y2=ax+b2过(15,38)、(0,20),
列方程组得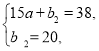
解得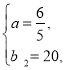
∴y2=![]() x+20,
x+20,
②当15<x≤20时,由由图象知:y1=kx+b1过(15,40)、(20,25),
列方程组得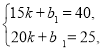
解得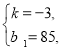
∴y1=-3x+85,
由图象知:y2=ax+b2过(15,38)、(20,20),
列方程组得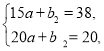
解得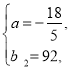
综上所述:每天包装红糖的质量随天数变化的函数关系式:
![]()
每天包装白糖的质量随天数变化的函数关系式:
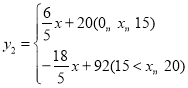
(3)设第x天销售的总利润为W元,
①当0≤x≤15时,
W=(6﹣3.9﹣0.5)y1+(8﹣5.5﹣0.5)y2=1.6y1+2y2=1.6(x+25)+2(1.2x+20)=4x+80.
由题意4x+80>120,∴x>10,∴x的取值范围为10<x≤15,
由题意知x=11,12,13,14,15;
②当15<x≤20时,
W=(6﹣3.9﹣0.5)y1+(8﹣5.5﹣0.5)y2=1.6y1+2y2=1.6(﹣3x+85)+2(![]() )=﹣12x+320.
)=﹣12x+320.
由题意得:﹣12x+320>120,∴x<![]() ,∴x的取值范围为15<x<
,∴x的取值范围为15<x<![]() .
.
由题意知x=16.
由①②可知在第11,12,13,14,15,16天中销售白糖和红糖的总利润大于120元.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:初中数学 来源: 题型:
【题目】“半日走遍江淮大地,安徽风景尽在徽园”,位于省会合肥的徽园景点某年三月共接待游客![]() 万人,四月比三月旅游人数增加了
万人,四月比三月旅游人数增加了![]() ,五月比四月游客人数增加了
,五月比四月游客人数增加了![]() ,已知三月至五月徽园的游客人数平均月增长率为
,已知三月至五月徽园的游客人数平均月增长率为![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,![]() ).
).
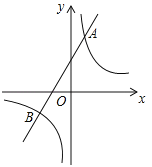
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲转盘被分成3个面积相等的扇形,乙转盘被分成2个半圆,每一个扇形或半圆都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转一次,直到指针指向一个区域为止).
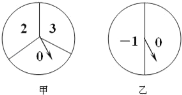
(1)请你用画树状图或列表格的方法,列出所有等可能情况,并求出点(x,y)落在坐标轴上的概率;
(2)直接写出点(x,y)落在以坐标原点为圆心,2为半径的圆内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,AD=6,E为AB边上一点,将△BEC沿CE翻折,点B落在点F处,当△AEF为直角三角形时,BE=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
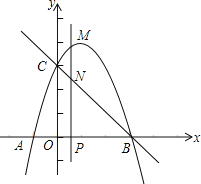
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点(点A在点B的左侧),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,求线段MN的最大值;
(3)是否存在点P,使得以点C、O、M、N为顶点的四边形是平行四边形?若存在,请直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究机构对本地区18-20岁的大学生就某个问题做随机调查,要求被调查者从A、B、C、D四个选项中选择自己赞同的一项,并将结果绘制成两幅不完整的统计图(如图):
大学生就某个问题调查结果统计表 | 大学生就某个问题调查结果扇形统计图 | ||||||||||||
|
|
请结合图中信息解答以下问题:
(1)m=_____,b=_____.
(2)若该地区18~20岁的大学生有1.2万人,请估计这些大学生中选择赞同A选项的人数:
(3)该研究机构决定从选择“C”的人中随机抽取2名进行访谈,而选择“C”的这4人中只有一名男性,求这名男性刚好被抽取到的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )
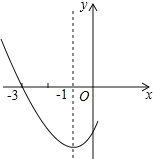
A.①②B.②③C.①②④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com