
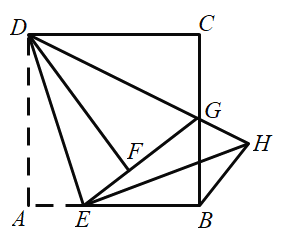
【题目】如图,在正方形ABCD中,E为边AB上一点,沿DE将![]() 折叠得到
折叠得到![]() ,延长EF交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
,延长EF交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)探求BH与AE数量关系,并说明理由.
【答案】(1)见解析;(2)![]() ,理由见解析
,理由见解析
【解析】
(1)根据对称得△ADE≌△FDE,再由HL证明Rt△DFG≌Rt△DCG,可得结论;
(2)作如图辅助线,构建全等三角形,证明△ADE≌△PEH,得AD=PE,AE=PH,再说明△BPH是等腰直角三角形,即可得结论.
(1)∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°,
∵沿DE将![]() 折叠得到
折叠得到![]() ,
,
∴△ADE≌△FDE,
∴DA=DF=DC,∠DFE=∠A=90°,
∴∠DFG=90°,
在Rt△DFG和Rt△DCG中,
![]() ,
,
∴Rt△DFG≌Rt△DCG(HL),
∴GF=GC;
(2)![]() ,
,
理由如下:过点H作HP⊥AB,垂足为P,

由(1)知,∠ADE=∠FDE,∠FDG=∠CDG,
∵∠ADC=90°,
∴∠EDG=45°,
∵EH⊥DE,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴DE=EH,
∵∠ADE+∠AED=∠AED+∠PEH=90°,
∴∠ADE=∠PEH,
在△ADE和△PEH中,
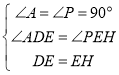 ,
,
∴△ADE≌△PEH,
∴AD=PE,AE=PH,
∴AD=AB=EP,
∴AE=BP=PH,
∴△BPH为等腰直角三角形,
∴![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
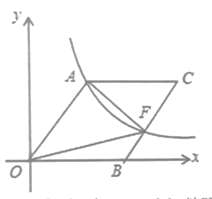
【题目】如图,在直角坐标系中,四边形OACB为菱形,OB在x轴的正半轴上,∠AOB=60°,过点A的反比例函数y= ![]() 的图像与BC交于点F,则△AOF的面积为 ______________.
的图像与BC交于点F,则△AOF的面积为 ______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的顶点A(1,1),B(3,1),规定把△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,这样连续经过2020次变换后,等边△ABC的顶点C的坐标为( )

A.(-2 020,![]() )B.(-2 019,
)B.(-2 019,![]() )
)
C.(-2 018,![]() )D.(-2 017,
)D.(-2 017,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
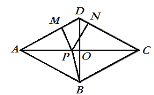
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,![]() ).
).
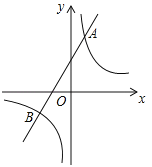
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交直线AB于点D,连接CD.若∠ABC=40°,∠ACD=30°,则∠BAC的度数为_____.
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交直线AB于点D,连接CD.若∠ABC=40°,∠ACD=30°,则∠BAC的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,AD=6,E为AB边上一点,将△BEC沿CE翻折,点B落在点F处,当△AEF为直角三角形时,BE=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
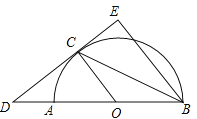
【题目】如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com