
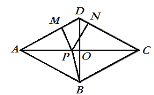
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于_________ .
【答案】7.8
【解析】
在△ADO中,由勾股定理可求得AD=5,由AC⊥BD,AO=CO,可知DO是AC的垂直平分线,由线段垂直平分线的性质可知AD=DC;利用面积法可证得PM+PN为定值,当PB最短时,PM+PN+PB有最小值,由垂线的性质可知当点P与点O重合时,OB有最小值.
∵AC⊥BD于点O,AO=CO=4,BO=DO=3,
∴在Rt△AOD中,
AD=![]() ,
,
∵AC⊥BD于点O,AO=CO,
∴CD=AD=5,
如图所示:连接PD,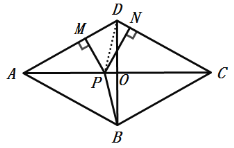
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴PM+PN=4.8,
∴当PB最短时,PM+PN+PB有最小值,
∵由垂线段最短可知:当BP⊥AC时,PB最短.
∴当点P与点O重合时,PM+PN+PB有最小,最小值=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】为了做好开学准备,某校共购买了20桶A、B两种桶装消毒液,进行校园消杀,以备开学.已知A种消毒液300元/桶,每桶可供2 000米2的面积进行消杀,B种消毒液200元/桶,每桶可供1 000米2的面积进行消杀.
(1)设购买了A种消毒液x桶,购买消毒液的费用为y元,写出y与x之间的关系式,并指出自变量x的取值范围;
(2)在现有资金不超过5 300元的情况下,求可消杀的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考查学生的综合素质,某市决定:九年级毕业生统一参加中考实验操作考试,根据今年的实际情况,中考实验操作考试科目为:![]() (物理)、
(物理)、![]() (化学)、
(化学)、![]() (生物),每科试题各为
(生物),每科试题各为![]() 道,考生随机抽取其中
道,考生随机抽取其中![]() 道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
(1)小明抽到化学实验的概率为 ;
(2)若只从考试科目考虑,小明和小丽抽到不同科目的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
的图像与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
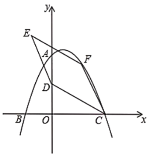
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图像上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图像上时,请直接写出此时S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
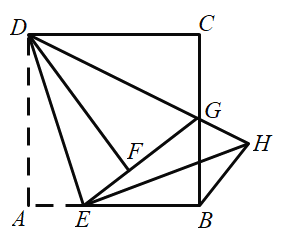
【题目】如图,在正方形ABCD中,E为边AB上一点,沿DE将![]() 折叠得到
折叠得到![]() ,延长EF交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
,延长EF交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)探求BH与AE数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
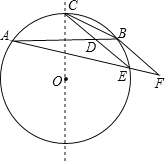
【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1:![]() ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售一批衬衫,每天可售出20件,每件盈利40元,为了扩大销售,减少库存,决定采取适当的降价措施,经调查发现,如果一件衬衫每降价1元,每天可多售出2件.
(1)若商场每天要盈利1200元,每件应降价多少元?
(2)设每件降价x元,每天盈利y元,每件降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
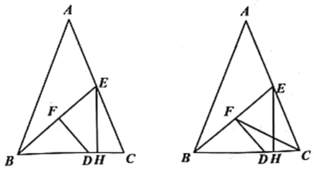
【题目】已知:如图1,△ABC中,AB=AC,BC=6,BE为中线,点D为BC边上一点;BD=2CD,DF⊥BE于点F,EH⊥BC于点H.
(1)CH的长为_____;
(2)求BF·BE的值:
(3)如图2,连接FC,求证:∠EFC=∠ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com