【题目】为了考查学生的综合素质，某市决定：九年级毕业生统一参加中考实验操作考试，根据今年的实际情况，中考实验操作考试科目为：
（物理）、
（化学）、
（生物），每科试题各为
道，考生随机抽取其中
道进行考试．小明和小丽是某校九年级学生，需参加实验考试．
（1）小明抽到化学实验的概率为 ；
（2）若只从考试科目考虑，小明和小丽抽到不同科目的概率为多少？
冲刺100分1号卷系列答案科目：初中数学 来源： 题型：
【题目】如图，直线y＝x+c与x轴交于点A（﹣4，0），与y轴交于点C，抛物线y＝﹣x2+bx+c经过点A，C．
（1）求抛物线的解析式；
（2）已知点P是抛物线上的一个动点，并且点P在第二象限内，过动点P作PE⊥x轴于点E，交线段AC于点D．
①如图1，过D作DF⊥y轴于点F，交抛物线于M，N两点（点M位于点N的左侧），连接EF，当线段EF的长度最短时，求点P，M，N的坐标；
②如图2，连接CD，若以C，P，D为顶点的三角形与△ADE相似，求△CPD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）课本情境:如图，已知矩形AOBC，AB＝6cm，BC＝16cm，动点P从点A出发，以3cm/s的速度向点O运动，直到点O为止；动点Q同时从点C出发，以2cm/s的速度向点B运动，与点P同时结束运动，出发 时，点P和点Q之间的距离是10cm；
（2）逆向发散:当运动时间为2s时，P，Q两点的距离为多少？当运动时间为4s时，P，Q两点的距离为多少？
（3）拓展应用：若点P沿着AO→OC→CB移动，点P，Q分别从A，C同时出发，点Q从点C移动到点B停止时，点P随点Q的停止而停止移动，求经过多长时间△POQ的面积为12cm2？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等边△ABC的顶点A(1，1)，B(3，1)，规定把△ABC“先沿x轴翻折，再向左平移1个单位”为一次变换，这样连续经过2020次变换后，等边△ABC的顶点C的坐标为（ ）
A.(－2 020，
)B.(－2 019，
)
C.(－2 018，)D.(－2 017，)
查看答案和解析>>
科目：初中数学 来源： 题型：
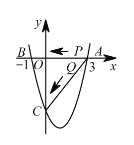
【题目】如图，二次函数
的图象与
轴交于
，
，与
轴交于点
．若点
，
同时从
点出发，都以每秒
个单位长度的速度分别沿
，
边运动，其中一点到达端点时，另一点也随之停止运动．
（1）直接写出二次函数的解析式；
（2）当，运动到
秒时，将△APQ沿
翻折，若点恰好落在抛物线上
点处，求出点坐标；
（3）当点运动到
点时，点停止运动，这时，在轴上是否存在点
，使得以，，为顶点的三角形为等腰三角形?若存在，请直接写出 点坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
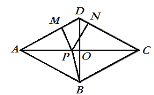
【题目】如图所示，四边形ABCD中，AC⊥BD于点O，AO=CO=4，BO=DO=3，点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M，作PN⊥DC于点N. 连接PB，在点P运动过程中，PM+PN+PB的最小值等于_________ .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在平面直角坐标系中，抛物线
与x轴相交于点A，B，与y轴相交于点C，直线y=-x-4经过A，C两点，
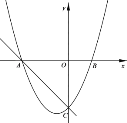
（1）求抛物线的表达式；
（2）如果点P，Q在抛物线上（P点在对称轴左边），且PQ∥AO，PQ=
AO，求P，Q的坐标；
（3）动点M在直线y=-x-4上，且以C，O，M为顶点的三角形与△ABC相似，求点M的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
