
【题目】如图,![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() .得到
.得到![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .
.
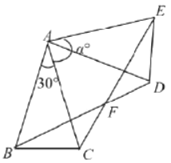
(1)求证:![]() ;
;
(2)用![]() 表示
表示![]() 的度数;
的度数;
(3)若使四边形![]() 是菱形,求
是菱形,求![]() 的度数,
的度数,
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:初中数学 来源: 题型:
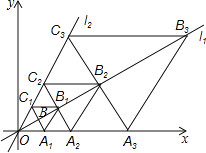
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() ,直线
,直线![]() ,在直线
,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,以点
,以点![]() 为对称中心,作点
为对称中心,作点![]() 的对称点
的对称点![]() ,过点
,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 轴于点
轴于点![]() ,作
,作![]() ∥
∥![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,得到四边形
,得到四边形![]() ;再以点
;再以点![]() 为对称中心,作
为对称中心,作![]() 点的对称点
点的对称点![]() ,过点
,过点![]() 作
作 ![]() ∥
∥![]() ,交
,交![]() 轴于点
轴于点![]() ,作
,作![]() ∥
∥![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,得到四边形
,得到四边形![]() ;…;按此规律作下去,则四边形
;…;按此规律作下去,则四边形![]() 的面积是___________.
的面积是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
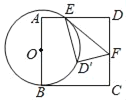
【题目】如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一边长为![]() 的等边
的等边![]() 游乐场,某人从边
游乐场,某人从边![]() 中点
中点![]() 出发,先由点
出发,先由点![]() 沿平行于
沿平行于![]() 的方向运动到
的方向运动到![]() 边上的点
边上的点![]() ,再由
,再由![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,又由点
,又由点![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,则此人至少要运动_______
,则此人至少要运动_______![]() ,才能回到点
,才能回到点![]() .如果此人从
.如果此人从![]() 边上意一点出发,按照上面的规律运动,则此人至少走______
边上意一点出发,按照上面的规律运动,则此人至少走______![]() ,就能回到起点.
,就能回到起点.
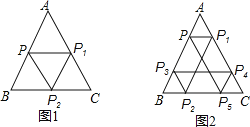
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考查学生的综合素质,某市决定:九年级毕业生统一参加中考实验操作考试,根据今年的实际情况,中考实验操作考试科目为:![]() (物理)、
(物理)、![]() (化学)、
(化学)、![]() (生物),每科试题各为
(生物),每科试题各为![]() 道,考生随机抽取其中
道,考生随机抽取其中![]() 道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
(1)小明抽到化学实验的概率为 ;
(2)若只从考试科目考虑,小明和小丽抽到不同科目的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“危险废物”,处理不当将污染环境.某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭做一次简单随机抽样调查.
(1)下列选取样本的方法最合理的一种是____________.(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
经抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:
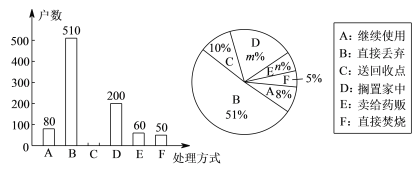
(2)填空:m=______,n=_____;
(3)补全条形统计图;
(4)该市市民家庭处理过期药品最常见的方式是 .(只填序号)
(5)家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
的图像与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
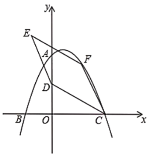
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图像上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图像上时,请直接写出此时S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数![]() 的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
(1)求反比例函数![]() 和直线OE的函数解析式;
和直线OE的函数解析式;
(2)求四边形OAFC的面积?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com