
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ��0��8������B������Ϊ����4��0��.
��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ��0��8������B������Ϊ����4��0��.
��1����ö��κ����ı���ʽ����C�����ꣻ
��2����D������Ϊ��0��4������FΪ�ö��κ����ڵ�һ������ͼ���ϵĶ��㣬����CD��CF����CD��CFΪ�ڱ���ƽ���ı���CDEF����ƽ���ı���CDEF�����ΪS.
����S�����ֵ��
���ڵ�F���˶������У�����E���ڸö��κ���ͼ����ʱ����ֱ��д����ʱS��ֵ.
���𰸡���1��![]() ��
��![]() ����2����50��
����2����50��![]()
��������
��1����A���B���������![]() �õ�����b��c�ķ����飬Ȼ��ⷽ�������b��c���ɵõ������ߵĽ���ʽ��Ȼ����㺯��ֵΪ0ʱ��Ӧ���Ա�����ֵ���ɵõ�C������
�õ�����b��c�ķ����飬Ȼ��ⷽ�������b��c���ɵõ������ߵĽ���ʽ��Ȼ����㺯��ֵΪ0ʱ��Ӧ���Ա�����ֵ���ɵõ�C������
��2��������DF��OF����ͼ����![]() ������S�ı���OCFD
������S�ı���OCFD![]()
![]() �����������������ʽ�õ�S��CDF=
�����������������ʽ�õ�S��CDF=![]() �������ö��κ��������ʵõ���CDF����������ֵ��Ȼ�����ƽ���ı��ε����ʿɵ�S�����ֵ��
�������ö��κ��������ʵõ���CDF����������ֵ��Ȼ�����ƽ���ı��ε����ʿɵ�S�����ֵ��
�������ı���CDEFΪƽ���ı��Σ���CD��EF��CD=EF������C���D�������������жϵ�C����ƽ��8����λ��������ƽ��4����λ�õ���D�����F����ƽ��8����λ��������ƽ��4����λ�õ���E����![]() ��Ȼ���
��Ȼ���![]() ���������߽���ʽ�õ�����t�ķ��̣��ٽⷽ�����t������CDF��������Ӷ��õ�S��ֵ��
���������߽���ʽ�õ�����t�ķ��̣��ٽⷽ�����t������CDF��������Ӷ��õ�S��ֵ��
�⣺��1����![]() ��
��![]() ����
����![]() �ã�
�ã�
![]() ��
��
���![]()
���������ߵĽ���ʽΪ![]()
��![]() ʱ��
ʱ��![]() �����
�����![]() ��
��![]()
����![]() ������Ϊ
������Ϊ![]()
��2��������![]() ����ͼ����
����ͼ����![]()
��![]()
��![]()
![]()
![]()
��![]() ʱ��
ʱ��![]() ����������ֵ�����ֵΪ25
����������ֵ�����ֵΪ25
���ı���![]() Ϊƽ���ı���
Ϊƽ���ı���
��![]() �����ֵΪ50
�����ֵΪ50
�ڡ��ı���![]() Ϊƽ���ı���
Ϊƽ���ı���
��![]() ��
��![]()
�ߵ�![]() ����ƽ��8����λ��������ƽ��4����λ�õ���
����ƽ��8����λ��������ƽ��4����λ�õ���![]()
���![]() ����ƽ��8����λ��������ƽ��4����λ�õ���
����ƽ��8����λ��������ƽ��4����λ�õ���![]() ����
����![]()
��![]() ����������
����������
��![]() �����
�����![]()
��![]() ʱ��
ʱ��![]()
���ʱ![]() ��
��


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
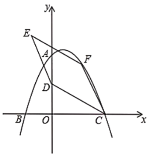
����Ŀ����ͼ1����ABC�͡�DEC��Ϊ���������Σ��ҡ�ACB=��DCE=90��������BE��AD�������߶����ڵ�ֱ�߽��ڵ�P.
��1���߶�BE��AD�к�������ϵ��λ�ù�ϵ����˵�����ɣ�
��2������֪BC=12��DC=5����DEC�Ƶ�C˳ʱ����ת��
����ͼ2������Dǡ������BC���ӳ�����ʱ����AP�ij���
������תһ�ܵĹ����У����PAB�����ΪS����S����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת
����ʱ�뷽����ת![]() ���õ�
���õ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
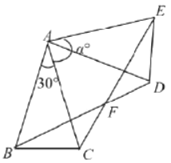
��1����֤��![]() ��
��
��2����![]() ��ʾ
��ʾ![]() �Ķ�����
�Ķ�����
��3����ʹ�ı���![]() �����Σ���
�����Σ���![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ��
��![]() ͬʱ��
ͬʱ��![]() �����������ÿ��
�����������ÿ��![]() ����λ���ȵ��ٶȷֱ���
����λ���ȵ��ٶȷֱ���![]() ��
��![]() ���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
��1��ֱ��д�����κ����Ľ���ʽ��
��2����![]() ��
��![]() �˶���
�˶���![]() ��ʱ������APQ��
��ʱ������APQ��![]() ���ۣ�����
���ۣ�����![]() ǡ��������������
ǡ��������������![]() �㴦�����
�㴦�����![]() �����ꣻ
�����ꣻ
��3������![]() �˶���
�˶���![]() ��ʱ����
��ʱ����![]() ֹͣ�˶�����ʱ����
ֹͣ�˶�����ʱ����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() ��
��![]() ��
��![]() Ϊ�����������Ϊ����������?�����ڣ���ֱ��д��
Ϊ�����������Ϊ����������?�����ڣ���ֱ��д��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
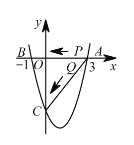
����Ŀ���������ij������ɽ�廬�£��侯�ܶ��ɳ�һ���侯սʿǰ������. ��Сʱ�ڶ���ǰȥ֧Ԯ��ƽ���ٶ��ǵ�һ�ӵ�1.5�����������ͬʱ�����֪���նӵij������������ľ���Ϊ90ǧ������������·����ͬ�������ӵ�ƽ���ٶȷֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı���ABCD�У�AC��BD�ڵ�O��AO=CO=4��BO=DO=3����PΪ�߶�AC�ϵ�һ������.����P�ֱ���PM��AD�ڵ�M����PN��DC�ڵ�N. ����PB���ڵ�P�˶������У�PM+PN+PB����Сֵ����_________ .
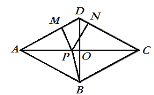
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼʾ���κ���y=ax2+bx+c�ĶԳ�����y����Ҳ࣬��ͼ����x�ύ�ڵ�A����1��0�����C��x2��0��������y�ύ�ڵ�B��0����2����Сǿ�õ����½��ۣ���0��a��2������1��b��0����c=��1������|a|=|b|ʱx2��![]() ��1�����Ͻ�������ȷ���۵����Ϊ ��
��1�����Ͻ�������ȷ���۵����Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�칫��¥һ��ǽ�������ͼ��ʾ��ͼ����ƣ����ͼ�����ĸ�ȫ�ȵ�ֱ�������κ�һ��С������ƴ�Ӷ��ɵĴ������Σ���С�����εı߳�m��ֱ�������ν϶̱߳�n����n��2m��4���������ε����ΪS��
��1����S����m�ĺ�����ϵʽ��
��2����С�����α߳�������3������������������ʱ����m��ֵ��
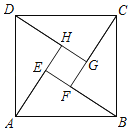
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
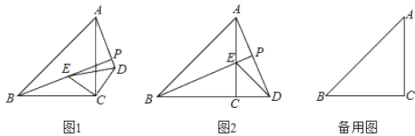
����Ŀ����ͼ���ڱ߳�Ϊ1��С��������ɵ������У������˸���ABC(����Ϊ�����ߵĽ���)��
(1)����ABC������ƽ��3����λ���ȣ�������ƽ��4����λ���Ⱥ�õ���A1B1C1������ƽ�ƺ��ͼ�Σ�
(2)����ABC�Ƶ�A1˳ʱ����ת90����õ���A2B2C2��������ת���ͼ�Σ�
(3)�������������̶�ֱ��������A1B1C1������A1D1(��ͼ��Ҫ�����ҹؼ���ķ���)��
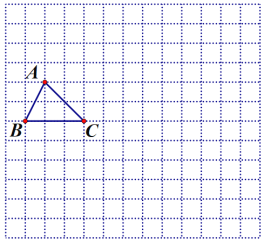
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com