
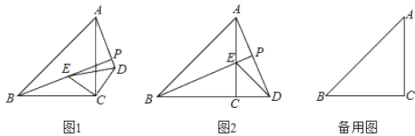
【题目】如图1,△ABC和△DEC均为等腰三角形,且∠ACB=∠DCE=90°,连接BE,AD,两条线段所在的直线交于点P.
(1)线段BE与AD有何数量关系和位置关系,请说明理由.
(2)若已知BC=12,DC=5,△DEC绕点C顺时针旋转,
①如图2,当点D恰好落在BC的延长线上时,求AP的长;
②在旋转一周的过程中,设△PAB的面积为S,求S的最值.
【答案】(1)BE=AD,BE与AD互相垂直,证明详见解析;(2)①AP=![]() ;②最小47,最大72
;②最小47,最大72
【解析】
(1)由题意根据等腰三角形的性质以及全等三角形的判定与性质,进行分析与等量代换即可;
(2)①由题意根据解直角三角形的勾股定理以及相似三角形的判定与性质进行分析即可;
②由∠APB=90°可知点P在以AB为直径的圆的一段弧上,且当BP与以CE为半径⊙C相切时,点P在其运动路径所在弧的两个端点处,P到AB的距离最小,此时△PAB的面积S最小;当点P与点C重合时,P到AB的距离最大,此时△PAB的面积S最大.
解:(1)BE=AD,BE与AD互相垂直;
证明:∵等腰△ABC,等腰Rt△DEC,
∴AC=BC,DC=EC,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE,
∴BE=AD,∠CAD=∠CBE,
∵∠CAD+∠APB=∠CBE+∠ACB=∠AOB,
∴∠APB=∠ACB=90°,即BE与AD互相垂直.
(2)①∵AB=BC=12,DC=EC=5,
∴AE=AC-EC=12-5=7,
Rt△BCE中,BE=![]() ,
,
由(1)同理可知∠APB=∠ACB=90°,∠CAD=∠CBE,
∴△APE∽△BCE,
∴![]() ,即
,即![]() ,解得AP=
,解得AP=![]() .
.
②由∠APB=90°可知点P在以AB为直径的圆的一段弧上,且当BP与以CE为半径⊙C相切时,点P在其运动路径所在弧的两个端点处,P到AB的距离最小,此时△PAB的面积S最小。如图1、2,易知四边形PDCE是边长为5的正方形.
∴ BE=AD=![]() ,BP=BE+PE=
,BP=BE+PE=![]() ,AP=AD-PD=
,AP=AD-PD=![]() ,
,
∴S(最小值)=![]() ×AP×BP=
×AP×BP=![]() ,
,
当点P与点C重合时,P到AB的距离最大,此时△PAB的面积S最大,如图3
S(最大值)=![]() ×AC×BC=
×AC×BC=![]() ×12×12=72.
×12×12=72.



科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.
,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=![]() ,小亮通过观察得出了下面四条信息:①
,小亮通过观察得出了下面四条信息:①![]() ,②abc<0,③4a+2b+c>0,④2a+3b=0.你认为其中正确的有_________________.
,②abc<0,③4a+2b+c>0,④2a+3b=0.你认为其中正确的有_________________.
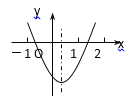
A.①②B.②④C.①③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与直线
与直线![]() 有两个不同的交点,其中一个交点在线段
有两个不同的交点,其中一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),另一个交点在线段
两个端点),另一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),则
两个端点),则![]() 的取值范围是
的取值范围是
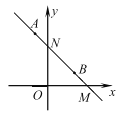
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了做好开学准备,某校共购买了20桶A、B两种桶装消毒液,进行校园消杀,以备开学.已知A种消毒液300元/桶,每桶可供2 000米2的面积进行消杀,B种消毒液200元/桶,每桶可供1 000米2的面积进行消杀.
(1)设购买了A种消毒液x桶,购买消毒液的费用为y元,写出y与x之间的关系式,并指出自变量x的取值范围;
(2)在现有资金不超过5 300元的情况下,求可消杀的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
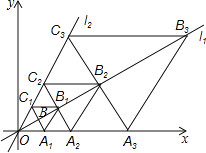
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() ,直线
,直线![]() ,在直线
,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,以点
,以点![]() 为对称中心,作点
为对称中心,作点![]() 的对称点
的对称点![]() ,过点
,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 轴于点
轴于点![]() ,作
,作![]() ∥
∥![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,得到四边形
,得到四边形![]() ;再以点
;再以点![]() 为对称中心,作
为对称中心,作![]() 点的对称点
点的对称点![]() ,过点
,过点![]() 作
作 ![]() ∥
∥![]() ,交
,交![]() 轴于点
轴于点![]() ,作
,作![]() ∥
∥![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,得到四边形
,得到四边形![]() ;…;按此规律作下去,则四边形
;…;按此规律作下去,则四边形![]() 的面积是___________.
的面积是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
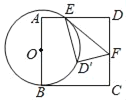
【题目】如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
的图像与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
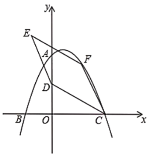
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图像上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图像上时,请直接写出此时S的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com