【题目】在平面直角坐标系中，点A（
，1）在射线OM上，点B（，2）在射线ON上，以AB为直角边作Rt△ABA1，以BA1为直角边作第二个Rt△BA1B1，然后以A1B1为直角边作第三个Rt△A1B1A2，…，依次规律，得到Rt△B2019A2020B2020，则点B2020的纵坐标为_____．
【答案】22021
【解析】
根据题意，分别找到AB、A1B1、A2B2……及 BA1、B1A2、B2A3……线段长度递增规律即可.
点A、A1、A2、A3……A2020各点在正比例函数
的图象上
点B、B1、B2、B3……B2020各点在正比例函数
的图象上
两个函数相减得到横坐标不变的情况下两个函数图象上点的纵坐标的差为
①
当A（B）点横坐标为
时
由①AB＝1，则BA1＝，则点A1横坐标为
，B1点纵坐标为
当A1（B1）点横坐标为
，由①A1B1＝2，则B1A2＝
则点A2横坐标为
，B2点纵坐标为:
当A2（B2）点横坐标为
，由①A2B2＝4，则B2A3＝
则点A3横坐标为:
，B3点纵坐标为
依此类推
点B2020的纵坐标为22021，
故答案为：22021．
阅读快车系列答案科目：初中数学 来源： 题型：
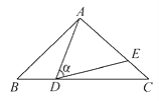
【题目】如图，在△ABC中，AB=AC=10，点D是边BC上一动点(不与B，C重合)，∠ADE=∠B=α，DE交AC于点E，且cosα=
．下列结论：①△ADE∽△ACD；②当BD=6时，△ABD与△DCE全等；③△DCE为直角三角形时，BD为8；④0<CE≤6.4．其中正确的结论是________．（把你认为正确结论的序号都填上）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ACB和Rt△AEF中，∠ACB＝∠AEF＝90°，若点P是BF的中点，连接PC，PE．
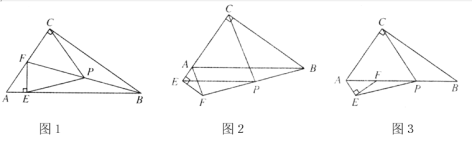
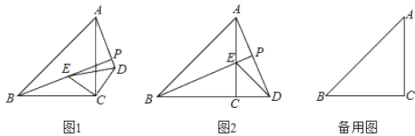
(1) 如图1，若点E，F分别落在边AB，AC上，求证：PC＝PE；
(2) 如图2，把图1中的△AEF绕着点A顺时针旋转，当点E落在边CA的延长线上时，探索PC与PE的数量关系，并说明理由．
(3) 如图3，把图2中的△AEF绕着点A顺时针旋转，点F落在边AB上．其他条件不变，问题(2)中的结论是否发生变化？如果不变，请加以证明；如果变化，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
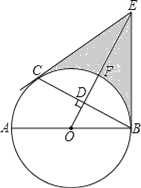
【题目】如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．
（1）求证：BE与⊙O相切；
（2）设OE交⊙O于点F，若DF=1，BC=2
，求阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与实践
在Rt△ABC中，∠ACB＝90°，点D为斜边AB上的动点（不与点A，B重合）．
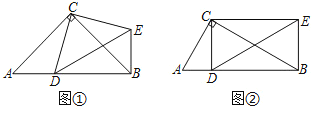
（1）操作发现：如图①，当AC＝BC＝8时，把线段CD绕点C逆时针旋转90°得到线段CE，连接DE，BE．
①∠CBE的度数为 ；
②当BE＝ 时，四边形CDBE为正方形；
（2）探究证明：如图②，当BC＝2AC时，把线段CD绕点C逆时针旋转90°后并延长为原来的两倍，记为线段CE，连接DE，BE．
①在点D的运动过程中，请判断∠CBE与∠A的大小关系，并证明；
②当CD⊥AB时，求证：四边形CDBE为矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于D．
（1）求证：△ADC∽△CDB；
（2）若AC=2，AB=
CD，求⊙O半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知A、B两点的坐标分别为（―2，0）,（0，1），⊙C的圆心坐标为（0，―1），半径为1．若D是⊙C上的一个动点，射线AD与y轴交于点E，则△ABE面积的最大值是( ) 
A. 4 B. 
C. 
D. 3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，△ABC和△DEC均为等腰三角形，且∠ACB=∠DCE=90°，连接BE，AD，两条线段所在的直线交于点P.
（1）线段BE与AD有何数量关系和位置关系，请说明理由．
（2）若已知BC=12，DC=5，△DEC绕点C顺时针旋转，
①如图2，当点D恰好落在BC的延长线上时，求AP的长；
②在旋转一周的过程中，设△PAB的面积为S，求S的最值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com