
����Ŀ����Rt��ACB��Rt��AEF�У���ACB����AEF��90��������P��BF���е㣬����PC��PE��
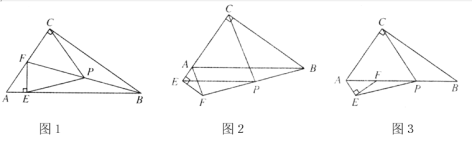
(1) ��ͼ1������E��F�ֱ����ڱ�AB��AC�ϣ���֤��PC��PE��
(2) ��ͼ2����ͼ1�еġ�AEF���ŵ�A˳ʱ����ת������E���ڱ�CA���ӳ�����ʱ��̽��PC��PE��������ϵ����˵�����ɣ�
(3) ��ͼ3����ͼ2�еġ�AEF���ŵ�A˳ʱ����ת����F���ڱ�AB�ϣ������������䣬����(2)�еĽ����Ƿ����仯��������䣬�����֤��������仯����˵�����ɣ�
���𰸡���1������������2��PC��PE�����ɼ���������3�����������ɼ�����
��������
��1������ֱ��������б�ߵ����ߵ���б�ߵ�һ�룬���ɣ�
��2�����жϡ�CBP�ա�HPF��������ֱ��������б�ߵ����ߵ���б�ߵ�һ�룻
��3�����жϡ�DAF�ա�EAF�����жϡ�DAP�ա�EAP��Ȼ���ñ���ʽ���ɣ�
�⣺��1��֤������ͼ��
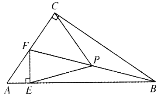
�ߡ�ACB����AEF��90����
���FCB����BEF��Ϊֱ�������Σ�
����P��BF���е㣬
��CP��![]() BF��EP��
BF��EP��![]() BF��
BF��
��PC��PE��
��2��PC��PE�������£�
��ͼ2���ӳ�CP��EF���ڵ�H��
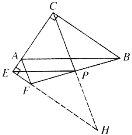
�ߡ�ACB����AEF��90����
��EH//CB��
���CBP����PFH����H����BCP��
����P��BF���е㣬
��PF��PB��
���CBP�ա�HFP(AAS)��
��PC��PH��
�ߡ�AEF��90����
����Rt��CEH��EP��![]() CH��
CH��
��PC��PE��
��3��(2)�еĽ��ۣ���Ȼ��������PC��PE���������£�
��ͼ3������F��FD��AC�ڵ�D������P��PM��AC�ڵ�M������PD��
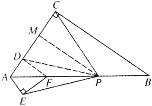
�ߡ�DAF����EAF����FDA����FEA��90����
����DAF����EAF��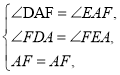
���DAF�ա�EAF(AAS)��
��AD��AE��
����DAP�ա�EAP�У�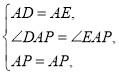
���DAP�ա�EAP (SAS)��
��PD��PF��
��FD��AC��BC��AC��PM��AC��
��FD//BC//PM��
��![]() ��
��
����P��BF���е㣬
��DM��MC��
����PM��AC��
��PC��PD��
�֡�PD��PE��
��PC��PE��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC��б��AB��y���ϣ���AC��x�ύ�ڵ�D��AEƽ����BAC����BC�ڵ�E��������A��D��E��Բ��Բ��Fǡ����y���ϣ���F��y���ཻ����һ��G��
��1����֤��BC����F�����ߣ�
��2������A��D������ֱ�ΪA��0����1����D��2��0��������F�İ뾶��
��3����̽���߶�AG��AD��CD����֮������ĵ�����ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
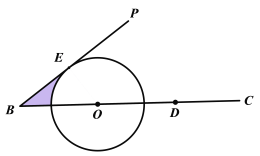
����Ŀ����ͼ����֪��PBC��������BC����ȡһ��D�����߶�BD���е�OΪԲ������O���ҡ�O��PB�����ڵ�E��
(1)����������BP��һ��A��ʹ��ABDΪ���������Σ���AB=AD����Ҫ������ֱ�ߺ�Բ�棬������ͼ�ۼ�����д������
(2)��֤��AD�ǡ�O�����ߣ�
(3)��BD�ij�Ϊ8cm����PBC=30�㣬����Ӱ���ֵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧ�˳߹���ͼ��ͨ����������������һ����ACD�������������ǣ������߶�AB���ֱ���A��BΪԲ�ģ�AB��Ϊ�뾶�����������Ľ���ΪC������BΪԲ�ģ�AB��Ϊ�뾶������AB���ӳ����ڵ�D��������AC��BC��CD������˵������ȷ���ǣ�������

A.��A��60��B.��ACD��ֱ��������
C.BC��![]() CDD.��B����ACD������
CDD.��B����ACD������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
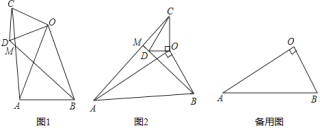
����Ŀ����1�����ⷢ��:��ͼ��1��������OAB����OCD�У�OA��OB��OC��OD����AOB����COD��36��������AC��BD���ڵ�M����![]() ��ֵΪ�� �����ڡ�AMB�Ķ���Ϊ�� ����
��ֵΪ�� �����ڡ�AMB�Ķ���Ϊ�� ����
��2�����̽�� :��ͼ��2��������OAB����OCD�У���AOB����COD��90������OAB����OCD��30��������AC����BD���ӳ����ڵ�M�������![]() ��ֵ����AMB�Ķ�����
��ֵ����AMB�Ķ�����
��3����չ����:�ڣ�2���������£�����OCD�Ƶ�O��ƽ������ת��AC��BD����ֱ�߽��ڵ�M����OD��1��OB��![]() ����ֱ��д������C���M�غ�ʱAC�ij���
����ֱ��д������C���M�غ�ʱAC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������������һ���µ���ʵ�����ģ�������������Ҫ40�����깤�����ס��ҹ�ͬ����20���Ӻ������ٵ�������20���Ӳ����깤.
�����ҵ����������ٷ����깤��
������������Ҫ����������ʱ�䲻����30���ӣ���������������ٷ��Ӳ����깤��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��![]() ��1��������OM�ϣ���B��
��1��������OM�ϣ���B��![]() ��2��������ON�ϣ���ABΪֱ�DZ���Rt��ABA1����BA1Ϊֱ�DZ����ڶ���Rt��BA1B1��Ȼ����A1B1Ϊֱ�DZ���������Rt��A1B1A2���������ι��ɣ��õ�Rt��B2019A2020B2020�����B2020��������Ϊ_____��
��2��������ON�ϣ���ABΪֱ�DZ���Rt��ABA1����BA1Ϊֱ�DZ����ڶ���Rt��BA1B1��Ȼ����A1B1Ϊֱ�DZ���������Rt��A1B1A2���������ι��ɣ��õ�Rt��B2019A2020B2020�����B2020��������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н�����������Ϊ���˽��һѧ��ÿѧ�ڲμ��ۺ�ʵ�����������������������ijУ��һѧ��һ��ѧ�ڲμ��ۺ�ʵ��������������õõ������ݻ���������������������ͳ��ͼ����ͼ����
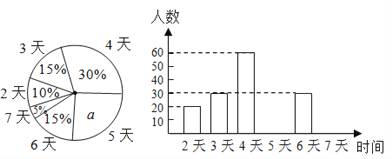
�������ͼ���ṩ����Ϣ���ش��������⣺
��1���������ͳ��ͼ��a��ֵ���������У��һѧ��������
��2���ֱ�����ʱ��Ϊ5�졢7���ѧ������������ȫƵ���ֲ�ֱ��ͼ��
��3���������ͳ��ͼ�����ʱ��Ϊ4��������������Բ�ĽǵĶ�����
��4������γ��������У���������λ���ֱ��Ƕ��٣�
��5��������й��г�һѧ��6000�ˣ�����������ʱ�䲻����4�����Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2��bx��c�ĶԳ�����x��![]() ��С��ͨ���۲�ó�������������Ϣ����
��С��ͨ���۲�ó�������������Ϣ����![]() ����abc<0����4a+2b+c>0����2a+3b=0������Ϊ������ȷ����_________________��
����abc<0����4a+2b+c>0����2a+3b=0������Ϊ������ȷ����_________________��
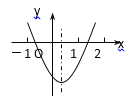
A.�٢�B.�ڢ�C.�٢�D.�ۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com