
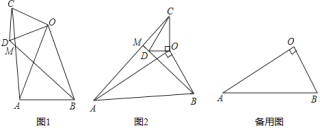
【题目】(1)问题发现:如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=36°,连接AC,BD交于点M.①![]() 的值为 ;②∠AMB的度数为 ;
的值为 ;②∠AMB的度数为 ;
(2)类比探究 :如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算![]() 的值及∠AMB的度数.
的值及∠AMB的度数.
(3)拓展延伸:在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M.若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
【答案】(1)①1;②36°;(2)![]() =
=![]() ,∠AMB=90°;(3)3
,∠AMB=90°;(3)3![]() 或4
或4![]() .
.
【解析】
(1)①由∠AOB=∠COD推出∠COA=∠DOB,利用边角边即可证△COA与△DOB全等,即可求出结果;
②先证出∠CAO与∠DBO相等,分别加∠AOB,∠AMB,结果仍相等,即可得到∠AOB=∠AMB=36°;
(2)证明△DOB与△COA相似即可求出AC:BD的值,再通过对顶角相等及∠OBD=∠CAO即可证出∠AMB的度数为90°;
(3)分点M在直线OA的左侧和右侧两种情况讨论,利用相似三角形对应边的比设未知数,在Rt△AMB中利用勾股定理构造方程即可求出AC的长.
解:(1)①∵∠AOB=∠COD=36°,
∴∠AOB+∠DOA=∠COD+∠DOA,
∴∠COA=∠DOB,
又∵OA=OB,OC=OD,
∴△COA≌△DOB(SAS),
∴AC=BD,
∴![]() =1,
=1,
故答案为:1;
②设AO与BD交于点E,
由①知,△COA≌△DOB,
∴∠CAO=∠DBO,
∵∠AOB+∠DBO=∠DEO,
∠AMB+∠CAO=∠DEO,
∴∠AOB=∠AMB=36°,
故答案为:36°;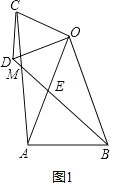
(2)在△OAB和△OCD中,
∵∠AOB=∠COD=90°,∠OAB=∠OCD=30°,
∴tan30°=![]() ,
,
∵∠AOB+∠DOA=∠COD+∠DOA,
即∠DOB=∠COA,
∴△DOB∽△COA,
∴![]() ,
,
∠DBO=∠CAO,
∵∠DBO+∠OEB=90°,∠OEB=∠MEA,
∴∠CAO+∠MEA=90°,
∴∠AMB=90°,
∴![]() =
=![]() ,∠AMB=90°;
,∠AMB=90°;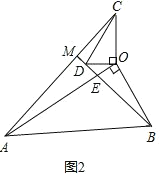
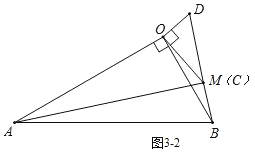
(3)①如图3-1,当点M在直线OB左侧时,
在Rt△OCD中,∠OCD=30°,OD=1,
∴CD=2,
在Rt△OAB中,∠OAB=30°,OB=![]() ,
,
∴AB=2![]() ,
,
由(2)知,∠AMB=90°,且![]() =
=![]() ,
,
∴设BD=x,则AC=AM=![]() x,
x,
在Rt△AMB中,
AM2+MB2=AB2,
∴(![]() x)2+(x+2)2=(2
x)2+(x+2)2=(2![]() )2,
)2,
解得,x1=3,x2=-4(舍去),
∴AC=AM=3![]() ;
;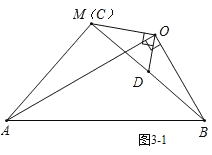
②如图3-2,当点M在直线OB右侧时,
在Rt△AMB中,
AM2+MB2=AB2,
∴(![]() x)2+(x-2)2=(2
x)2+(x-2)2=(2![]() )2,
)2,
解得,x1=4,x2=-3(舍去),
∴AC=AM=4![]() ,
,
综上所述,AC的长为3![]() 或4
或4![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
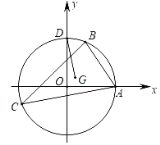
【题目】如图,半径为3的⊙O分别与x轴,y轴交于A,D两点,⊙O上两个动点B,C,使∠BAC=45°恒成立,设△ABC的重心为G,则DG的最小值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
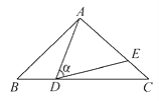
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是________.(把你认为正确结论的序号都填上)
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,AB=8,∠B=120°,沿过菱形不同的顶点裁剪两次,再将所裁下的图形拼接,若恰好能无缝,无重叠的拼接成一个矩形,则所得矩形的对角线长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.
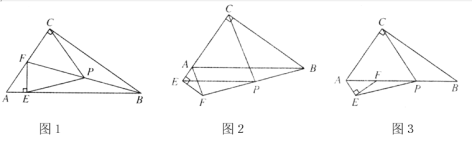
(1) 如图1,若点E,F分别落在边AB,AC上,求证:PC=PE;
(2) 如图2,把图1中的△AEF绕着点A顺时针旋转,当点E落在边CA的延长线上时,探索PC与PE的数量关系,并说明理由.
(3) 如图3,把图2中的△AEF绕着点A顺时针旋转,点F落在边AB上.其他条件不变,问题(2)中的结论是否发生变化?如果不变,请加以证明;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
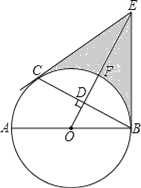
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB=![]() CD,求⊙O半径.
CD,求⊙O半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
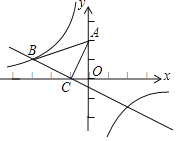
【题目】如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(﹣1,0),tan∠ACO=2.一次函数y=kx+b的图象经过点B、C,反比例函数y=![]() 的图象经过点B.
的图象经过点B.
(1)求一次函数关系式和反比例函数的关系式;
(2)当x<0时,kx+b﹣![]() <0的解集为 ;
<0的解集为 ;
(3)若x轴上有两点E、F,点E在点F的左边,且EF=1.当四边形ABEF周长最小时,请直接写出点E的横坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com