
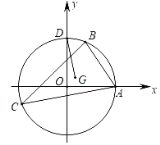
【题目】如图,半径为3的⊙O分别与x轴,y轴交于A,D两点,⊙O上两个动点B,C,使∠BAC=45°恒成立,设△ABC的重心为G,则DG的最小值是_______.
【答案】![]() .
.
【解析】
连接AG并延长,交BC于点F,由三角形ABC的重心为G,可知F为BC的中点,再由垂径定理可知OF⊥BC,从而可求得OF的长;在AO上取点E,使AE=2EO,连接GE,可判定三角形AGE相似于三角形AFO,由相似三角形的性质列出比例式,求得GE的长,进而可得点E的坐标,利用勾股定理求出DE的长,根据G在以E为圆心,2为半径的圆上运动,可知DG的最小值为DE的长减去,计算即可.
解:连接AG并延长,交BC于点F.
∵△ABC的重心为G
∴F为BC的中点,
∴OF⊥BC,
∵∠BAC=45°
∴BOF=45°
∴OBF=45°
∴OF=BF=FC=![]()
∵△ABC的重心为G,
∴AG=![]() AF.
AF.
在AO上取点E,使AE=![]() AO,连接GE,
AO,连接GE,
∴E(1,0)
∵.![]()
∴△AGE∽△AFO,
∴![]()
∴GE=![]()
∴G在以E为圆心,![]() 为半径的圆上运动
为半径的圆上运动
∴DE=![]()
∴DG的最小值为![]() .
.



 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
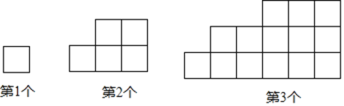
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
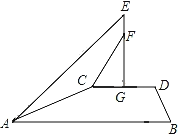
【题目】“行千里致广大”是重庆人民向大家发出的旅游邀请.如图,某建筑物上有一个旅游宣传语广告牌,小亮在A处测得该广告牌顶部E处的仰角为45°,然后沿坡比为5:12的斜坡AC行走65米至C处,在C处测得广告牌底部F处的仰角为76°,已知CD与水平面AB平行,EG与CD垂直,且EF=2米,则广告牌顶部E到CD的距离EG为( )(参考数据:sin76°≈0.97,cos76°≈0.24.tan76°≈4)
A.46B.44C.71D.69
查看答案和解析>>
科目:初中数学 来源: 题型:
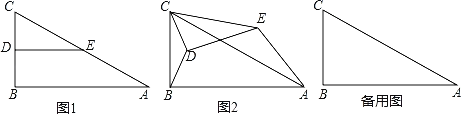
【题目】如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,![]() =_______;
=_______;
②当α=180°时,![]() =______.
=______.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发市场内有一种水果,保鲜期一周,如果冷藏,可以延长保鲜时间,但每天仍有一定数量的这种水果变质,假设这种水果保鲜期内的个体重量基本保持不变。现有一个体户,按市场价收购了这种水果200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后这种鲜水果每千克的价格每天可上涨0.2元,但存放一天需各种费用20元,日平均每天还有1千克变质丢弃.
(1)设![]() 天后每千克鲜水果的市场价
天后每千克鲜水果的市场价![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若存放![]() 天后将鲜水果一次性出售,设鲜水果的销售总金额为
天后将鲜水果一次性出售,设鲜水果的销售总金额为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)该个体户将这批水果存放多少天后出售,可获最大利润![]() ?最大利润
?最大利润![]() 是多少?
是多少?
(本题不要求写出自变量![]() 的取值范围)
的取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:
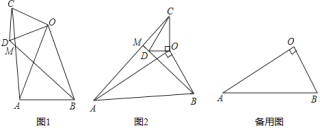
【题目】(1)问题发现:如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=36°,连接AC,BD交于点M.①![]() 的值为 ;②∠AMB的度数为 ;
的值为 ;②∠AMB的度数为 ;
(2)类比探究 :如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算![]() 的值及∠AMB的度数.
的值及∠AMB的度数.
(3)拓展延伸:在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M.若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com