
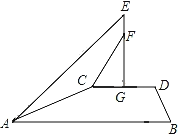
【题目】“行千里致广大”是重庆人民向大家发出的旅游邀请.如图,某建筑物上有一个旅游宣传语广告牌,小亮在A处测得该广告牌顶部E处的仰角为45°,然后沿坡比为5:12的斜坡AC行走65米至C处,在C处测得广告牌底部F处的仰角为76°,已知CD与水平面AB平行,EG与CD垂直,且EF=2米,则广告牌顶部E到CD的距离EG为( )(参考数据:sin76°≈0.97,cos76°≈0.24.tan76°≈4)
A.46B.44C.71D.69
【答案】A
【解析】
作CM⊥AB于M,延长EG交AB于N,根据矩形的性质得到GN=CM,MN=CG,根据坡度的概念求出AM、CM,根据等腰直角三角形的性质列式求出CG,结合图形计算即可.
解:作CM⊥AB于M,延长EG交AB于N,
则GN⊥AB,
∴四边形CMNG为矩形,
∴GN=CM,MN=CG,
斜坡AC的坡比为5:12,
则CM=5x,AM=12x,
由勾股定理得,(5x)2+(12x)2=652,
解得,x=5,
∴CM=5x=25,AM=12x=60,
在Rt△FCG中,tan∠FCG=![]() ,即
,即![]() =tan76°=4,
=tan76°=4,
∴FG=4CG,
∵∠EAN=45°,
∴AN=EN,即60+CG=2+4CG+25,
解得,CG=11,
∴FG=44,
∴EG=EF+FG=46(米)
故选:A.



 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】[问题情境]
我们知道数轴上的两点A、B的距离|AB|=|xA-xB|,那么如果已知平面上两点P1(x1,y1),P2(x2,y2),如何求P1,P2的距离d(P1P2)呢?
下面我们就来研究这个问题.
问题 一般地,已知平面上两点P1(x1,y1),P2(x2,y2),如何求点P1和P2的距离?
答: 当x1≠x2,y1=y2时,|P1P2|=|x2-x1|;
当x1=x2,y1≠y2时,|P1P2|=|y2-y1|;
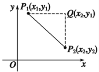
当x1≠x2,y1≠y2时,如图,
在Rt△P1QP2中,由勾股定理知,
|P1P2|2=|P1Q|2+|QP2|2,所以d(P1,P2)=|P1P2|=![]() .
.
归纳:两点P1(x1,y1),P2(x2,y2)间的距离公式d(P1,P2)=|P1P2|=![]() .
.
解决问题:
(1)已知A(2,-4),B(-2,3),求d(A,B)
(2)已知点A(1,2),B(3,4),C(5,0),求证:△ABC是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一辆汽车在高速公路上行驶的平均速度比在普通公路上行驶的平均速度提高80%,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上行驶的平均速度是多少千米∕小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按如下步骤作图:
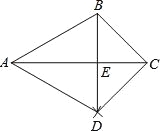
(1)以A圆心,AB长为半径画弧;
(2)以C为圆心,CB长为半径画弧,两弧相交于点D;
(3)连接BD,与AC交于点E,连接AD,CD.
①四边形ABCD是中心对称图形;
②△ABC≌△ADC;
③AC⊥BD且BE=DE;
④BD平分∠ABC.
其中正确的是( )
A.①② B.②③ C.①③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.
(1)求从中随机抽取出一个黑球的概率是多少?
(2)若往口袋中再放入x个白球和y个黑球,从口袋中随机取出一个白球的概率是![]() ,求y与x之间的函数关系式;
,求y与x之间的函数关系式;
(3)若在(2)的条件下,放入白球x的范围是0<x<4(x为整数),求y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借鉴我们已有的研究函数的经验,探索函数y=|x2﹣2x﹣3|﹣2图象和性质,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 10 | m | ﹣2 | 1 | n | 1 | ﹣2 | 3 | 10 | … |
其中,m= ,n= ;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
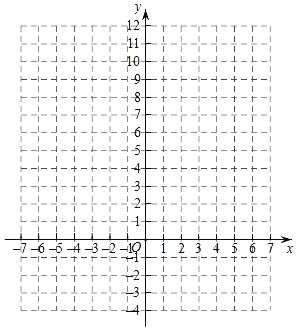
(3)观察函数图象:
①当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根时,根据函数图象直接写出b的取值范围为 .
②在该平面直角坐标系中画出直线y=![]() x+2的图象,根据图象直接写出该直线与函数y=|x2﹣2x﹣3|﹣2的交点横坐标为: (结果保留一位小数).
x+2的图象,根据图象直接写出该直线与函数y=|x2﹣2x﹣3|﹣2的交点横坐标为: (结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
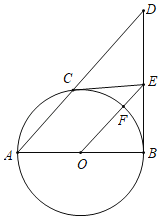
【题目】如图,AB为⊙O的直径,DB⊥AB于B,点C是弧AB上的任一点,过点C作⊙O的切线交BD于点E.连接OE交⊙O于F.
(1)求证:CE=ED;
(2)填空:
①当∠D= 时,四边形OCEB是正方形;
②当∠D= 时,四边形OACF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
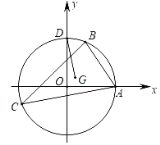
【题目】如图,半径为3的⊙O分别与x轴,y轴交于A,D两点,⊙O上两个动点B,C,使∠BAC=45°恒成立,设△ABC的重心为G,则DG的最小值是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com