
【题目】如图,AB为⊙O的直径,DB⊥AB于B,点C是弧AB上的任一点,过点C作⊙O的切线交BD于点E.连接OE交⊙O于F.
(1)求证:CE=ED;
(2)填空:
①当∠D= 时,四边形OCEB是正方形;
②当∠D= 时,四边形OACF是菱形.
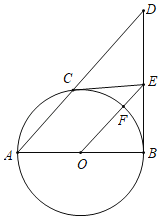
【答案】(1)见解析;(2)①45°;②30°
【解析】
(1)证明:连接OC,由CE为⊙O的切线,可得OC⊥CE,∠OCE=90°,所以∠ACO+∠DCE=90°,因为BD⊥AB,所以∠A+∠D=90°,又OA=OC,∠A=∠OCA,所以∠D=∠DCE,因此CE=ED;
(2)①若四边形OCEB是正方形,则∠CEB=90°,∠CED=90°,因为CE=ED,所以∠D=∠DCE=45°;
②若四边形OACF是菱形,则OA=AC,又OA=OC,于是△OAC为等边三角形,∠A=60°,因为DB⊥AB,所以∠A+∠D=90°,因此∠D=30°.
解:(1)证明:连接OC,
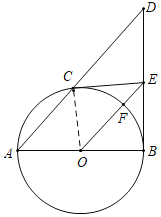
∵CE为⊙O的切线,
OC⊥CE,
∴∠OCE=90°,
∴∠ACO+∠DCE=90°,
∵BD⊥AB,
∴∠ABD=90°,
∴∠A+∠D=90°,
∵OA=OC,
∴∠A=∠OCA,
∴∠D=∠DCE,
∴CE=ED;
(2)若四边形OCEB是正方形,
则∠CEB=90°,
∴∠CED=90°,
∵CE=ED,
∴∠D=∠DCE=45°,
故答案为45°;
(3)若四边形OACF是菱形,
则OA=AC,
∵OA=OC,
∴△OAC为等边三角形,
∴∠A=60°,
∵DB⊥AB,
∴∠A+∠D=90°,
∴∠D=90°﹣60°=30°,
故答案为:30°.


科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“行千里致广大”是重庆人民向大家发出的旅游邀请.如图,某建筑物上有一个旅游宣传语广告牌,小亮在A处测得该广告牌顶部E处的仰角为45°,然后沿坡比为5:12的斜坡AC行走65米至C处,在C处测得广告牌底部F处的仰角为76°,已知CD与水平面AB平行,EG与CD垂直,且EF=2米,则广告牌顶部E到CD的距离EG为( )(参考数据:sin76°≈0.97,cos76°≈0.24.tan76°≈4)
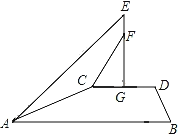
A.46B.44C.71D.69
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:
类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.

理解应用:
(1)请仿照上面的竖式方法计算:![]() ;
;
(2)已知两个多项式的和为![]() ,其中一个多项式为
,其中一个多项式为![]() .请用竖式的方法求出另一个多项式.
.请用竖式的方法求出另一个多项式.
(3)已知一个长为![]() ,宽为
,宽为![]() 的矩形
的矩形![]() ,将它的长增加8.宽增加
,将它的长增加8.宽增加![]() 得到一个新矩形
得到一个新矩形![]() ,且矩形
,且矩形![]() 的周长是
的周长是![]() 周长的3倍(如图).同时,矩形
周长的3倍(如图).同时,矩形![]() 的面积和另一个一边长为
的面积和另一个一边长为![]() 的矩形
的矩形![]() 的面积相等,求
的面积相等,求![]() 的值和矩形
的值和矩形![]() 的另一边长.
的另一边长.
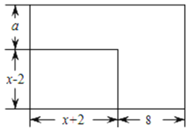
查看答案和解析>>
科目:初中数学 来源: 题型:
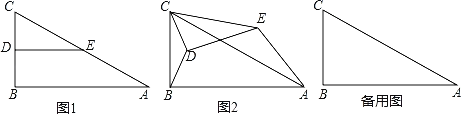
【题目】如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,![]() =_______;
=_______;
②当α=180°时,![]() =______.
=______.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距![]() 一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是
一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是![]() 以快车开始行驶计时,设时间为
以快车开始行驶计时,设时间为![]() , 两车之间的距离为
, 两车之间的距离为![]() ,图中的折线是
,图中的折线是![]() 与
与![]() 的函数关系的部分图象,根据图象解决以下问题:
的函数关系的部分图象,根据图象解决以下问题:

(1)慢车的速度是_ _![]() ,点
,点![]() 的坐标是_ _;
的坐标是_ _;
(2)线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数关系式是_ ;
之间的函数关系式是_ ;
(3)试在图中补全点![]() 以后的图象.
以后的图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com